Regelbundet yttre mått

Från Rilpedia

Version från den 6 maj 2009 kl. 21.52 av Calle (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Regelbundet yttre mått är ett koncept inom matematik, mer specifikt måtteori. Ett regelbundet yttre mått är ett mått om varje mängd kan approximeras med en mätbar mängd.

Innehåll

Definition

I måtteori är ett yttre mått 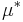\mu^*\, i rummet 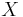X\, regelbundet om det för varje 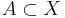A \subset X finns en 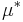\mu^*\,-mätbar mängd 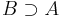B \supset A så att

\mu^* (A) = \mu (B)\,..

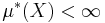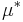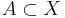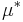Om \mu^* (X) < \infty och \mu^*\, är regelbundnet kan man visa att A \subset X är \mu^*\,-mätbar om och endast om

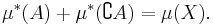\mu^* (A) + \mu^* (\complement A) = \mu (X)..

Borelregelbundna yttre mått

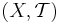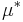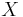Om (X,\mathcal{T})\, är ett topologiskt rum så är ett yttre mått \mu^*\, i X\, ett Borelregelbundet yttre mått om det för varje 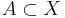A \subset X finns en Borelmängd 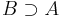B \supset A så att

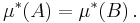\mu^* (A) = \mu^* (B)\,..

Exempel

Yttre Lebesguemåttet och Yttre Hausdorfmåttet är regelbundna och Borelregelbundna.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Regelbundet_yttre_m%C3%A5tt"
Personliga verktyg