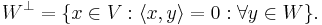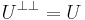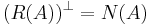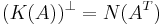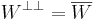Ortogonalt komplement

Från Rilpedia

Version från den 3 maj 2009 kl. 22.30 av Calle (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Ett ortogonalt komplement är inom matematikområdena linjär algebra och funktionalanalys en benämning på ett underrum 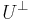$U^\bot$ i ett inre produktrum $V$ som består av alla de element som är ortogonala mot alla elementen i ett givet underrum $U$ :

$W^\bot = \{x \in V: \langle x, y \rangle = 0: \forall y \in W \}.$

Ändlig dimension

I ett ändligtdimensionellt inre produktrum av dimension n är det ortogonala komplementet till ett k-dimensionellt underrum ett underrum av dimension $n - k$ . Det ortogonala komplementet av det ortogonala komplementet är det ursprungliga rummet:

$U^{\bot\bot} = U$

För en m × n-matris, så har kolonnrummet, $K (A)$ , nollrummet, $N (A)$ , och radrummet , $R (A)$ , följande egenskaper:

$(R(A))^\bot = N(A)$

$(K(A))^\bot = N(A^T)$

Egenskaper

Det ortogonala komplementet är alltid en sluten mängd i den metriska topologin, för ändligtdimensionella inre produktrum är detta en enkel följd av att alla underrum är slutna. I oändlighetsdimensionella Hilbertrum finns det underrum som inte är slutna, men deras ortogonala komplement är slutna. Det är ortogonala komplementet till det ortogonala komplenetet av W blir då det slutna höljet av W:

$W^{\bot \bot} = \overline W$

Ortogonalt komplement

Från Rilpedia

Ändlig dimension

Egenskaper

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk