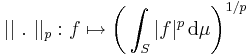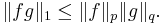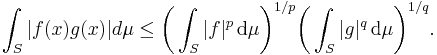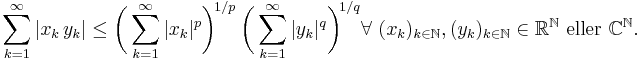Hölders olikhet

Från Rilpedia

Version från den 1 juni 2008 kl. 17.09 av Leo (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Ambox ?.svg
 Den här artikeln anses vara otydlig eller onödigt fackspråklig.
 Hjälp gärna till att förtydliga artikeln och göra den mer lättläst. Se eventuellt diskussionssidan för mer information.

Hölders olikhet är ett resultat inom den gren av matematik som kallas funktionalanalys. Olikheten kan ses som en generalisering av Cauchy-Schwarz olikhet, och är ett viktigt resultat i studiet av Lp-rum. Den används för att visa att Lp-rummen verkligen är normerade rum, vilket ges av Minkowskis olikhet, samt ett antal andra uppskattningar.

Formulering

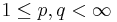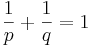Låt (S,Σ,μ) vara ett måttrum och låt 1 \leq p, q < \infty med \frac{1}{p} + \frac{1}{q} = 1 . För mätbara funktioner, reell- eller komplexvärda, definieras Lp-normen som

|| \ . \ ||_p : f \mapsto \biggl(\int_S |f|^p\,\mathrm{d}\mu\biggr)^{1/p}

Hölders olikhet ges nu av följande påstående:

\|fg\|_1 \le \|f\|_p \|g\|_q.

Detta kan också skrivas på integralform som

\int_S |f(x) g(x)| d\mu \leq \biggl(\int_S |f|^p\,\mathrm{d}\mu\biggr)^{1/p} \biggl(\int_S |g|^q\,\mathrm{d}\mu\biggr)^{1/q}.

Eftersom en oändlig summa även kan ses som en integral (om man låter man 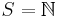S = \mathbb{N} och μ vara räknemåttet) så kan Hölders olikhet även formuleras för följder i 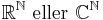\mathbb{R}^{\mathbb N}\text{ eller }\mathbb{C}^{\mathbb N} . Då fås följande olikhet:

\sum\limits_{k=1}^{\infty} |x_k\,y_k| \le \biggl( \sum_{k=1}^{\infty} |x_k|^p \biggr)^{\!1/p\;} \biggl( \sum_{k=1}^{\infty} |y_k|^q \biggr)^{\!1/q} \forall \, \, (x_k)_{k\in\mathbb N}, (y_k)_{k\in\mathbb N}\in\mathbb{R}^{\mathbb N}\text{ eller }\mathbb{C}^{\mathbb N}.

Kommentarer

I definitionen ovan betyder 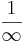\frac{1}{\infty} 0. För 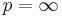p = \infty definieras uttrycket 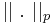|| \ . \ ||_p som

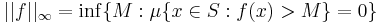||f||_{\infty} = \inf \{M : \mu\{x \in S: f(x) > M\} = 0\}, det vill säga infimum av 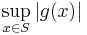\sup_{x \in S} |g(x)| , där g tillhör mängden av funktioner som är lika med f nästan överallt.
Hämtad från "https://sv.rilpedia.org/wiki/H%C3%B6lders_olikhet"
Personliga verktyg