Kontinuerlig funktion
Från Rilpedia
Det som är kontinuerligt är något som är utan avbrott, ett flytande sammanhang utan fasta hållpunkter, utan att vara uppdelat i steg. Motsats: diskret.
Inom matematiken är en storhet som är kontinuerlig en storhet som är sådan att man alltid kan finna en annan storhet som skiljer sig från den förra med en kvantitet som är mindre än någon ändlig storhet.
Topologi är den gren av matematiken som studerar kontinuerliga funktioner.
Innehåll |
Exempel
- En funktion definierad på en delmängd av de reella talen är kontinuerlig om den har ett gränsvärde för ett godtyckligt x=x0 i (det inre av) definitionsmängden, det vill säga om gränsvärdet
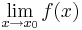existerar, och detta är lika med f(x0).
Definition av kontinuerlig funktion på reella tallinjen
En funktion f av en variabel är:
- kontinuerlig i punkten x om det för alla ε > 0 existerar ett δ > 0 sådant att |x-y| < δ medför |f(x)-f(y)| < ε.
- kontinuerlig i ett intervall [a, b] om den är kontinuerlig i alla punkter i intervallet.
Definition av kontinuerlig funktion mellan topologiska rum
För allmänna topologiska rum gäller att en funktion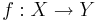 
är kontinuerlig då det för varje öppen mängd 
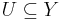gäller att f − 1(U) är öppen i X. Vi säger att f är kontinuerlig i punkten x om det för varje omgivning V till f(x) finns en omgivning U till x, sådan att 
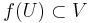. Om X och Y är metriska rum, är denna definition ekvivalent med den klassiska "ε − δ"definitionen:
Definition av kontinuerlig funktion mellan metriska rum
Om (X,dx),(Y,dy) är metriska rum är funktionen 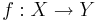kontinuerlig i x om det för alla ε > 0 existerar ett δ > 0 så att 
.
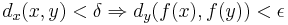Se även
