Topologi

Från Rilpedia

(Omdirigerad från Topologi (matematik))
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Broarna i Köningsberg är ett klassiskt topologiskt problem.

Topologi från grekiskans τοπος "topos", (plats, ställe), och λογος "logos", (lära), är en gren av den moderna matematiken som generaliserar begreppen öppna mängder och kontinuerliga funktioner.

Topologi föddes i början av 1900-talet och är därför ett relativt nytt område inom matematiken. Den har visat sig mycket användbar och tillämpas idag inom andra grenar av matematik såsom analys och algebra, såväl som inom andra vetenskaper som till exempel fysik och genetik.

Topologi introduceras ofta genom att först definiera "topologiska rum", sedan "kontinuerliga funktioner" mellan dessa rum. Därefter studerar man olika "topologiska egenskaper" hos dessa. Se definitioner nedan.

Innehåll

Definition

Ett topologiskt rum är ett par (X,T), där X är en mängd och T en samling av delmängder till X. Denna samling kallas för en topologi på X och definieras av följande tre egenskaper.

  1. Familjen T innehåller mängden X och den tomma mängden Ø.
  2. Familjen T är sluten under bildandet av godtyckliga unioner: Om 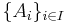\{A_i\}_{i\in I} är en godtycklig samling av mängder där varje mängd Ai tillhör familjen T, så är unionen 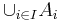\cup_{i\in I} A_i också ett element i familjen T.
  3. Familjen T är sluten under bildandet av ändliga snitt: Om 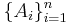\{A_i\}_{i=1}^n är en ändlig samling av mängder där varje mängd Ai tillhör samlingen T, så är snittet 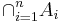\cap_{i=1}^n A_i också ett element i familjen T.

En delmängd A av X säges vara öppen med avseende på en topologi T, om A är ett element i familjen T. Om topologin är underförstådd i sammanhanget säger man bara att A är en öppen delmängd av X.

Exempel på topologiska rum

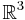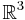  • Rummet \mathbb{R}^3 där de öppna mängderna är alla mängder som är öppna med avseende på någon metrik i \mathbb{R}^3,

exempelvis 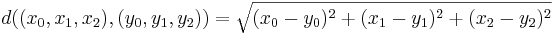d((x_0,x_1,x_2),(y_0,y_1,y_2)) = \sqrt{ (x_0 - y_0)^2 +(x_1 -y_1)^2 + (x_2-y_2)^2 } .

  • En mängd X med den triviala topologin T = {Ø, X}. Detta är den minsta möjliga topologin på X. Med avseende på denna topologi är det endast den tomma mängden, Ø, och mängden X själv, som är öppna mängder.
  • En mängd X med den diskreta topologin T = 2X. Mängden 2X kallas för potensmängden av X och består av samtliga delmängder till X. Detta är den största möjliga topologin på X. Med avseende på denna topologi är varje delmängd av X en öppen mängd.

Relaterade definitioner

  • En delmängd A av ett topologiskt rum (X,T) kallas sluten om dess komplementmängd 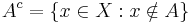A^c = \{x \in X : x \notin A\} är öppen, det vill säga mängden Ac är ett element i topologin T.
  • En kontinuerlig funktion 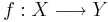f : X \longrightarrow Y från ett topologiskt rum (X,T) till ett topologiskt rum (Y,S) är en funktion som är sådan att mängden 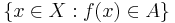\{x \in X : f(x) \in A\} är ett element i topologin T, oavsett vilken mängd A ur topologin S man än väljer.
    • Om man väljer den triviala topologin på Y så är det endast de konstanta funktionerna 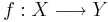f : X \longrightarrow Y som är kontinuerliga.
    • Om man väljer den diskreta topologin på Y så är varje funktion 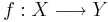f : X \longrightarrow Y kontinuerlig.
  • En homeomorfism från X till Y är en bijektiv kontinuerlig funktion sådan att dess invers också är kontinuerlig.
  • En topologisk egenskap, alternativt topologisk invariant, är en egenskap som bevaras under homeomorfismer. Exempel på sådana egenskaper är bland annat

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Topologi"
Personliga verktyg