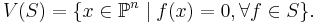Zariskitopologi
Från Rilpedia
Inom matematik är Zariskitopologin en topologi som brukar användas inom algebraisk geometri vid studiet av varieteter. Den infördes först av Oskar Zariski för att studera både affina varieteter och projektiva varieteter. När Alexander Grothendieck sedan reformerade den algebraiska geometrin infördes en modern definition.
Zariskitopologin är en mycket svag topologi, i den meningen att den inte kan separera punkter. Den är nämligen bara Hausdorff för varieteter över ändliga kroppar. Den ger därför inte heller speciellt mycket geometrisk information.
Klassisk definition
Låt k vara en algebraiskt sluten kropp. Zariskitopologin definieras ofta i termer av sina slutna mängder, i motsats till vad som är brukligt inom t ex matematisk analys. I affin algebraisk geometri, där varieteterna lever i ett affint rum, är en sluten mängd i Zariskitopologin en mängd på formen
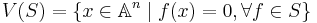där S är en mängd polynom i n variabler över k.
I projektiv algebraisk geometri måste Zariskitopologin definieras lite annorlunda. Detta beror på att en punkt i ett n-dimensionellt projektivt rum är en ekvivalensklass av punkter i ett n+1-dimensionellt affint rum, och olika representanter för samma punkt kan därför ge olika värden till ett polynom. För homogena polynom gäller däremot att värdet är samma för alla representanter, och man kan då definiera Zariskitopologin s slutna mängder som
där S är en mängd homogena polynom.
Modern definition
I modern algebraisk geometri utgår man från spektrum för en kommutativ ring. För ett ideal I definieras nu en sluten mängd i Zariskitopologin som 
där Spec betecknar spektrum för den kommutativa ringen A.
