Impulsmomentsatsen

Från Rilpedia

Version från den 12 juli 2007 kl. 15.47 av Yvwv (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Impulsmomentsatsen bygger på Reynolds transportteorem (RTT) där den extensiva storheten 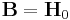\mathbf{B} = \mathbf{H}_0 och den intensiva storheten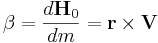 \mathbf{\beta} = { d \mathbf{H}_0 \over d m} = \mathbf{r} \times \mathbf{V}

där H är rörelsemängdsmomentet, r är en riktningsvektor, V är en hastighetsvektor och m är massa. Omskriven med ovanstående blir RTT:

\sum \mathbf{M}_0 = \sum \Big( \mathbf{r} \times \mathbf{F} \Big)_0 = {d \over dt} \Bigg[ \int_{kv} \Big( \mathbf{r} \times \mathbf{V} \Big) \rho dV \Bigg] + \int_{ky} \Big( \mathbf{V}_r \times \mathbf{n} \Big) dA

där F är en kraftvektor, kv är en kontrollvolym, ky är en kontrollyta, 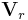\mathbf{V}_r är den relativa hastighetsvektorn och ρ är densiteten. Impulsmomentsatsen kan förenklas beroende på situation.

Fix kontrollvolym

\sum \mathbf{M}_0 = {d \over dt} \Bigg[ \int_{kv} \Big( \mathbf{r} \times \mathbf{V} \Big) \rho dV \Bigg] + \int_{ky} \Big( \mathbf{V} \times \mathbf{n} \Big) dA

Endimensionellt in- och utflöde

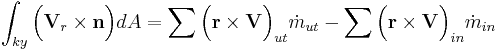
\int_{ky} \Big( \mathbf{V}_r \times \mathbf{n} \Big) dA = \sum \Big( \mathbf{r} \times \mathbf{V} \Big)_{ut} \dot{m}_{ut} - \sum \Big( \mathbf{r} \times \mathbf{V} \Big)_{in} \dot{m}_{in}

där 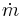\dot{m} står för massflödet.

Se även


Gnome-system-run.svg Denna mekanikartikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Impulsmomentsatsen"
Personliga verktyg