Geometrisk fördelning
Från Rilpedia
Version från den 5 maj 2009 kl. 02.57 av Xqbot (Diskussion)
Texten från svenska Wikipedia
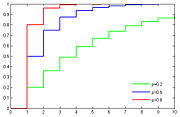
Geometriska fördelningen är en diskret sannolikhetsfördelning -- sannolikhetsfördelningen av antalet Bernoulliförsök som måste göras för att lyckas en gång, då varje försök lyckas med sannolikheten p. Sannolikheten att det första lyckade försöket sker vid försök n är:
P(X = n) = (1 − p)n − 1p
för n = 1, 2, 3, ...
Väntevärdet för en geomeriskt fördelad stokastisk variabel är 1/p och variansen är (1 − p)/p2.
Det är det specialfall av negativ binomialfördelning i vilket r = 1. Liksom den kontinuerliga motsvarigheten (exponentialfördelningen), är den geomeriska fördelningen "minneslös"; faktum är att det är den enda diskreta fördelningen som är minneslös.
Se även negativ binomialfördelning och hypergeometrisk fördelning.
