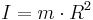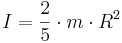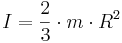Tröghetsmoment
Från Rilpedia
Tröghetsmoment, betecknas med I eller J, används för att beskriva stela kroppars dynamik. Tröghetsmomentet har samma roll i rotationsrörelser som massa har för translationsrörelse. Tröghetsmoment introducerades av Euler. Tröghetsmomentet är ett mått på motståndet att accelerera en kropps rotation kring en given axel.
Tröghetsmomentet beror av objektets form och hur massan är distribuerad i objektet,
där ri är avståndet från masselementet mi till exempelvis masscentrum. (Liksom moment varierar tröghetsmomentet beroende på referenssystemet, men genom att bestämma en kropps tröghetsmoment (med avseende på masscentrum) kan sedan parallellaxelsatsen,
- I0 = I + d2m,
användas för att omvandla tröghetsmomentet med avseende på godtycklig position med avståndet d från masscentrum.)
För kontinuerliga massdistributioner används integralen
dm är det kontinuerliga masselementet från ett volymselement,
- dm = ρdV,
där ρ är densiteten.
Tröghetstensorn
Tröghetsmoment i tre dimensioner beskrivs av andra ordningens tensor (matris) I = Iij:
För en stel kropp är tröghetstensorn summan av varje partikels moment: m → mi, R → Ri. Elementen Iii kallas för tröghetsmoment, medan elementen Iij, i ≠ j, kallas för tröghetsprodukter. Men det finns ett val av koordinatsystem så att tröghetsmomentet kan skrivas
Detta moment motsvarar ett koordinatsystem som sammanfaller med principalaxlarna. Genom att välja principalaxlar fås ett tröghetsmoment som bara innehåller diagonalelement. Alternativt kan tröghetsmomentet diagonaliseras för att hitta principalaxlarna.
Exempel
|
Cylinder med längden L, fastsatt i längdaxelns mitt: Samma stav, men fastsatt i ena ändpunkten: |
|
Rektangulär bricka med sidorna a och b, fastsatt i brickans mitt: |
|
En rektangulär bricka med längden L och försumbar bredd, fastsatt i ena ändan: |
|
Ett cylinderhjul med yttre radie R och inre radie r, fastsatt i dess ort: Ett massivt hjul (hjul inre radie r = 0):
Ett tunt hjul (med inre radie r ≈ R): |
|
Ett massivt klot med radie R, fastsatt så att rotationsaxeln går genom klotets centrum: Ett klotformat skal (klot med inre radie r ≈ R): |





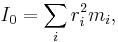
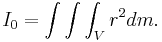
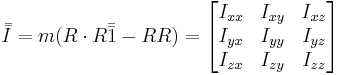
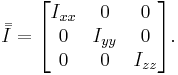
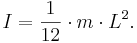
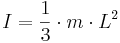
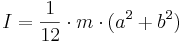
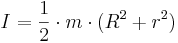
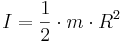 ,
,