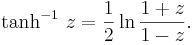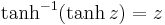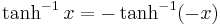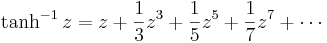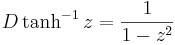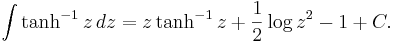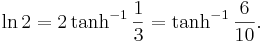Arctanh

Från Rilpedia

Version från den 23 november 2008 kl. 08.57 av LA2-bot (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Graf av funktionen y = tanh^-1(x).

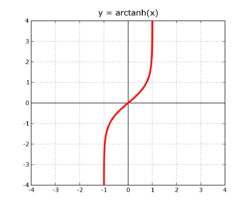
Den inversa hyperboliska tangenten (arcus tangens hyperbolicus, oftast betecknad arctanh, atanh eller tanh^-1) är en matematisk funktion, definierad som inversen till den hyperboliska tangenten. Dess värde ges av

$\tanh^{-1} \, z = \frac 1 2 \ln \frac{1+z}{1-z}.$

För reella tal är funktionen definierad i intervallet (-1, 1), där den är monotont växande.

Identiteter och egenskaper

Att funktionen är invers till den hyperboliska tangenten innebär att

$\tanh^{-1}(\tanh{z}) = z\,\!$

Den är en udda funktion:

$\tanh^{-1} x = -\tanh^{-1}(-x)\,\!$

Den har följande Maclaurinserie:

$\tanh^{-1} z = z + \frac{1}{3}z^3 + \frac{1}{5}z^5 + \frac{1}{7}z^7 + \cdots$

Den inversa hyperboliska tangenten har derivatan

$D \tanh^{-1} z = \frac{1}{1-z^2}$

vars enkla form gör att funktionen ibland dyker upp i integraler. Den obestämda integralen till funktionen själv ges av

$\int \tanh^{-1} z \, dz = z \tanh^{-1} z + \frac{1}{2} \log{z^2 - 1} + C.$

Tillämpningar

Den inversa hyperboliska tangenten är relaterad till logaritmen av 2 genom att

$\ln 2 = 2\tanh^{-1}\frac{1}{3} = \tanh^{-1}\frac{6}{10}.$

Analogt med Machins formel för π som bygger på den trigonometriska inversa tangenten, kan man härleda formler som får funktionens Maclaurinserie att konvergera mycket snabbt, och därmed gör det möjligt att effektivt beräkna ett stort antal siffror av logaritmen av 2. Gourdon och Sebah (2001) ger flera sådana formler, däribland

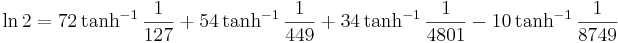$\ln 2 = 72 \tanh^{-1} \frac{1}{127} + 54 \tanh^{-1} \frac{1}{449} + 34 \tanh^{-1} \frac{1}{4801} -10 \tanh^{-1} \frac{1}{8749}$ .

Numeriska värden

z	tanh⁻¹(z)
0	0
0,1	0,10033534773107558064
0,2	0,20273255405408219099
0,3	0,30951960420311171547
0,4	0,42364893019360180686
0,5	0,54930614433405484570
0,6	0,69314718055994530942
0,7	0,86730052769405319443
0,8	1,0986122886681096914
0,9	1,4722194895832202300

Källor

Eric Weisstein. "Inverse Hyperbolic Tangent". MathWorld.
Xavier Gourdon & Pascal Sebah. "The logarithm constant: log 2".

Arctanh

Från Rilpedia

Innehåll

Identiteter och egenskaper

Tillämpningar

Numeriska värden

Källor

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk