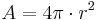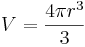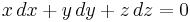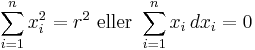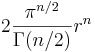Sfär
Från Rilpedia
En sfär är ytan på en klotformad kropp. Alla punkter på en sfär befinner sig på samma avstånd till sfärens centrum – detta avstånd kallas radie och betecknas r.
Sfärens area beräknas med formeln
och det tillhörande klotets volym är
I formeln motsvarar r sfärens radie. För den som vill lära sig formlerna utantill kan det underlätta att lägga på minnet att uttrycket för arean är volymuttryckets derivata med avseende på r.
Sfären är den minsta yta som omsluter störst volym. I naturen är exempelvis luftbubblor och vattendroppar (frånsett gravitation eller annan påverkan) sfäriska eftersom ytspänningen strävar efter att minimera ytan.
En cylinder som omsluter en sfär har en volym som är 3/2 gånger sfärens, vilket (tillsammans med formlerna för sfärens yta och volym) redan Arkimedes kände till.
Terminologi
Givet en punkt på sfären, så kallas den punkt som ligger precis mittemot den, på en rät linje genom centrum, för dess antipod. Den cirkel som ligger på sfären halvvägs mitt emellan två antipoder kallas en storcirkel, och är den cirkel på sfären som har störst radie. Denna storcirkel delar sfären i två halvklot, eller hemisfärer.
I likhet med jordytan betecknas ibland en speciell punkt på sfären för nordpol. Dess antipod kallas då sydpol, och storcirkeln mitt emellan kallas ekvator.
Ekvationer, generaliseringar
Inom analytisk geometri beskrivs punkterna som ingår i en sfär med radie r och centrum i punkten (x0, y0, z0) som alla punkter (x, y, z) i R3 sådana att
- (x − x0)2 + (y − y0)2 + (z − z0)2 = r2
Alternativt kan sfären beskrivas genom en differentialekvation:
Hypersfärer
Dessa beskrivningar låter sig även generaliseras till sfärer av andra dimensioner: en sfär i Rn kan då beskrivas med ekvationenerna
där  är koordinaterna för Rn. Man talar om "n-dimensionell hypersfär", eller "n-hypersfär".
är koordinaterna för Rn. Man talar om "n-dimensionell hypersfär", eller "n-hypersfär".
I synnerhet är då en sfär i ett 1-dimensionellt rum ett par punkter (r, -r), medan en sfär i ett 2-dimensionellt rum är en cirkel. Inom kosmologin är ett vanligt angreppssätt att betrakta universum som en 4-dimensionell hypersfär med tiden som radie och rummet som dess tredimensionella yta. På engelska kallas en sådan kropp ibland för glome, men 3-sphere är det vanligaste uttrycket.
Det visar sig att ytan av en sfär av radie r i ett n-dimensionellt euklidiskt rum rum (denna sfär kallas en (n-1)-dimensionell hypersfär) ges av formeln
där Γ är Eulers gammafunktion.