Klot

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Den här artikeln handlar om geometri. För tyget klot, se Klot (textil).

Ett klot är en tredimensionell solid kropp vars begränsningsyta är en sfär.

Klotets volym kan beräknas med formeln 4πr³/3 där r är klotets radie.

En cylinder som omsluter ett klot har en volym som är 3/2 gånger klotets, vilket (tillsammans med formlerna för sfärens yta och klotets volym) redan Arkimedes kände till.

Härledning av volymformeln

En halvcirkel med radie r och centrum i origo motsvarar följande funktion (se Pythagoras sats):

$f(x)=\sqrt{r^2-x^2}, x \in [-r, r]$

Motsvarande rotationskropp har då denna volym:

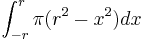
$\int_{-r}^{r}\pi(r^2-x^2) dx$

Vi börjar med att separera termerna:

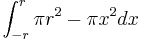
$\int_{-r}^{r}\pi r^2-\pi x^2 dx$

Dessa kan sedan integreras separat:

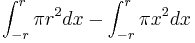
$\int_{-r}^{r}\pi r^2 dx - \int_{-r}^{r}\pi x^2 dx$

Motsvarande primitiva funktioner är triviala:

$\pi r^2\left[ x \right]_{-r}^{r} - \pi \left[ \frac{x^3}{3} \right]_{-r}^{r}$

Insättning av r och −r ger:

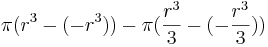
$\pi (r^3-(-r^3)) - \pi (\frac{r^3}{3} - (-\frac{r^3}{3}))$

Förenkling, steg 1:

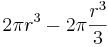
$2 \pi r^3 - 2\pi \frac{r^3}{3}$

Förenkling, steg 2:

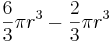
$\frac{6}{3} \pi r^3 - \frac {2}{3} \pi r^3$

Och det hela ger resultatet:

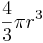
$\frac{4}{3} \pi r^3$

Klot i analytisk geometri

I analytisk geometri beskrivs klotet, placerat i ett kartesiskt koordinatsystem med ekvationen

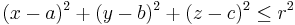
$(x-a)^2 + (y-b)^2 + (z-c)^2 \le r^2$

där (a, b, c) är klotets medelpunkt och r är dess radie.

Klot

Från Rilpedia

Härledning av volymformeln

Klot i analytisk geometri

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk