Weierstrassfunktionen
Från Rilpedia

Weierstrassfunktionen skapades av den tyske matematikern Karl Weierstrass under sin tid som professor i Berlin [1]. Den är ett exempel på att en överallt kontinuerlig funktion inte behöver vara deriverbar någonstans och har formen
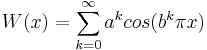
där 0<a<1 , 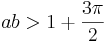 och b är ett udda heltal större än 1 [2].
och b är ett udda heltal större än 1 [2].
Innehåll |
Historia
Historiskt sett ligger Weierstrassfunktionens betydelse i att den var den första publicerade funktion som motsade att alla kontinuerliga funktioner är deriverbara överallt utom i ett visst antal diskreta punkter. Det hade dock skapats funktioner med dessa egenskaper tidigare, dock publicerades dessa aldrig vilket gjorde att de inte fick samma spridning som Weierstrassfunktionen. [2]. Weierstrassfunktionen anses också vara en av de första fraktalerna som skapats.
Bevis av kontinuitet
Eftersom
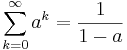
och
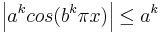
kommer funktionen vara kontinuerlig på hela 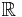 enligt Weierstrass majorantsats [2].
enligt Weierstrass majorantsats [2].
Bevis av icke-deriverbarhet
Bevisidé
Beviset, utförd enligt [2], bygger på att man ska bevisa att höger- och vänsterderivaten är olika, dvs att 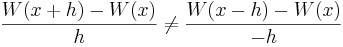
Börja med att låta 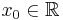 och
och 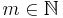 var två godtyckliga tal.
var två godtyckliga tal.
Välj 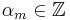 så att
så att ![b^m x_0 - \alpha \in \left( -\frac{1}{2}, \frac{1}{2} \right]](/w/images/sv.rilpedia.org/math/3/e/3/3e3e75d46c41bcdbe7e79a9a37817ad7.png)
och sätt 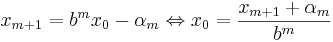
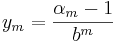 och
och 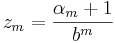 .
.
För att visa att ym < x0 < zm görs följande beräkningar:
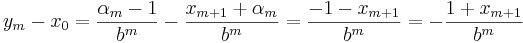
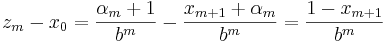
vilket ger olikheten
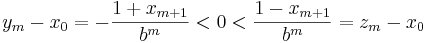
varför ym < x0 < zm.
Samtidigt fås att 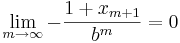 , dvs
, dvs 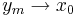 från vänster då
från vänster då 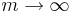
och 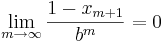 , dvs
, dvs 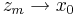 från höger då
från höger då 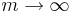 efter b>1.
efter b>1.
Uppskattning av vänsterderivatan
Den vänsterderivatan begrundas först och delas upp i S1 och S2 enligt
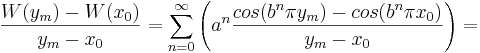
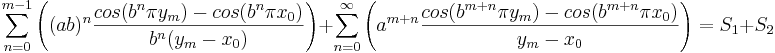 .
.
Där alltså S1 är summan av kvoterna från n=0 till n=m-1 och S2 är summan av kvoterna från n=m till oändligheten. S1 och S2 behandlas sedan var för sig för kunna uppskatta S1 uppåt och S2 nedåt.
Uppskattning av S1
S1 skrivs om med hjälp av den trigonometriska formeln 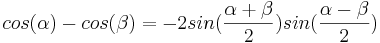
samt det faktum att 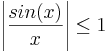 .
.
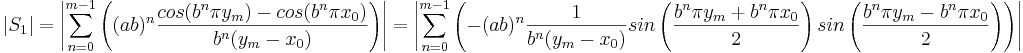
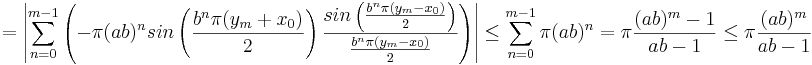
Uppskattning av S2
S2 kan, då b är ett udda heltal och 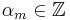 skrivas om enligt
skrivas om enligt
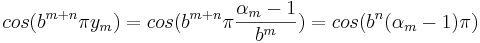
och
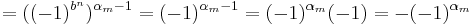
vilket ger
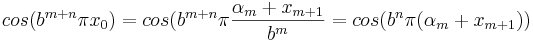
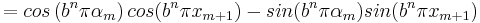
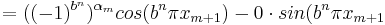
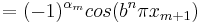 .
.
Vi får alltså att
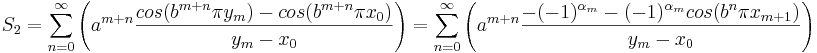
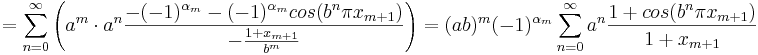 .
.
I och med att ![x_{m+1} \in \left( -\frac{1}{2}, \frac{1}{2} \right]](/w/images/sv.rilpedia.org/math/7/f/9/7f9270d40df289ff0154e40d6c63e54e.png) och
och 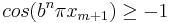
är alla termer positiva vilket ger att
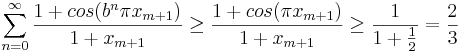 .
.
Resultat
Uppskattningarna av S1 och S2 ger att det existerar ett ![\epsilon_1 \in \left[ -1,1 \right]](/w/images/sv.rilpedia.org/math/d/e/f/def5d0d616718dbf225c7c991e274448.png) och η1 > 1 så att
och η1 > 1 så att
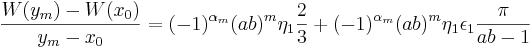
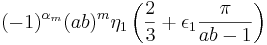 .
.
Uppskattning av högerderivatan
Högerderivatan uppskattas på samma sätt som den vänstra enligt
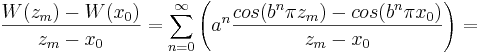
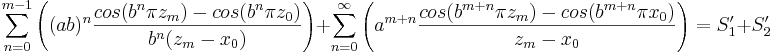 .
.
Uppskattning av S'1
S'1 skrivs om på samma sätt som S1.
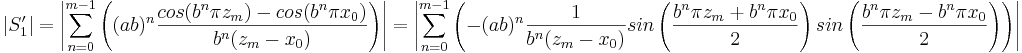
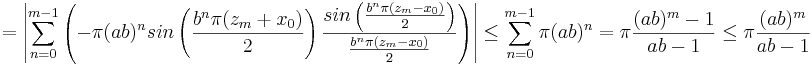
Uppskattning av S'2
S'2 kan uppskattas på samma sätt som S2 enligt nedan.
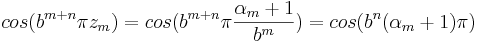
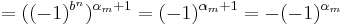
Från beräkningen av S2 fås även att
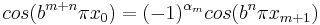
vilket ger att
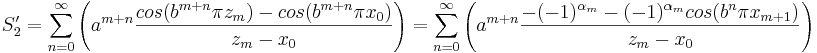
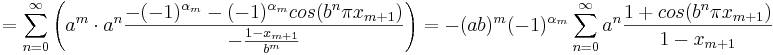 .
.
I och med att ![x_{m+1} \in \left( -\frac{1}{2}, \frac{1}{2} \right]](/w/images/sv.rilpedia.org/math/7/f/9/7f9270d40df289ff0154e40d6c63e54e.png) och
och 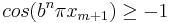
är alla termer positiva vilket ger att
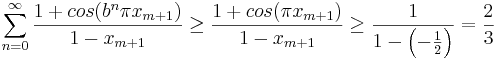 .
.
Resultat
Uppskattningarna av S'1 och S'2 ger att det existerar ett ![\epsilon_1 \in \left[ -1,1 \right]](/w/images/sv.rilpedia.org/math/d/e/f/def5d0d616718dbf225c7c991e274448.png) och η1 > 1 så att
och η1 > 1 så att
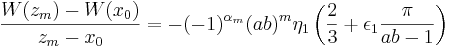
Slutsats
Vänster- och högerderivatan kan skrivas enligt:
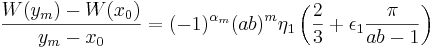
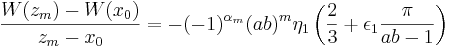
Detta tillsammans med att
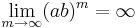
ger direkt att funktionen saknar derivata eftersom vänster- och högerderivatan har olika tecken.
Fotnoter
- ↑ Jan Thompson & Thomas Martinsson: Matematiklexikon, 1991. ISBN 91-46-16515-0.
- ↑ 2,0 2,1 2,2 2,3 http://epubl.luth.se/1402-1617/2003/320/LTU-EX-03320-SE.pdf