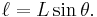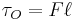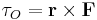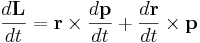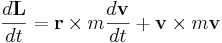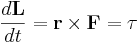Vridmoment
Från Rilpedia
Vridmoment eller kraftmoment är en krafts förmåga att vrida ett objekt kring en punkt. Det kan också beskrivas som den hävstångsverkan som kraften ger upphov till. Vridmomentet som är beroende av kraften på objektet och radien på hävarmen mellan objektet och punkten kring vilken vridningen sker. Storheten vridmoment betecknas ofta med den grekiska bokstaven 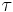 men andra bokstäver som M och N förekommer också. SI-enheten för vridmoment är newtonmeter (Nm). Vridmoment kan uttryckas antingen som en skalär- eller en vektoriell storhet.
men andra bokstäver som M och N förekommer också. SI-enheten för vridmoment är newtonmeter (Nm). Vridmoment kan uttryckas antingen som en skalär- eller en vektoriell storhet.
Innehåll |
Beräkning av vridmoment
Vridmomentet är proportionell mot kraften 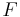 och mot momentarmen, det vill säga mot det vinkelräta avståndet
och mot momentarmen, det vill säga mot det vinkelräta avståndet 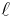 mellan kraftens verkningslinje och rotationscentrum O. Vridmomentet
mellan kraftens verkningslinje och rotationscentrum O. Vridmomentet 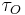 med avseende på O är alltså:
med avseende på O är alltså:
Med vektornotation kan vridmomentet med avseende på O tecknas som kryssprodukten av 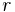 och
och 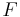 :
:
Om 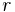 är en vektor refererad från en punkt O är
är en vektor refererad från en punkt O är 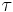 vridmomentet runt O. Om O är origo används ofta benämningen vridmomentet
vridmomentet runt O. Om O är origo används ofta benämningen vridmomentet 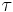 .
.
Hävarmen är lägesvektorn |r|. I det tvådimensionella fallet, med en kraft som appliceras vinkelrät till hävarmen, är momentet
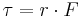 , där
, där- r är hävarmens längd (magnituden på lägesvektorn r)och
- F är kraften (magnituden på kraftvektorn F).
- τ är vridmomentet
Relation till rörelsemängdsmoment
Vridmomentet är ett mått på ändringen i rörelsemängdsmoment,
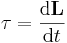 , där
, där- L är det vektoriella rörelsemängdsmomentet
- t är tid.
Därmed kommer vridmomentets vektor peka i samma riktning som den ändring i rörelsemängdsmomentets vektor som den orsakar (se figur). Speciellt förblir rörelsemängdsmomentet konstant om vridmomentet är lika med nollvektorn.
Relationen kan härledas från rörelsemängdsmomentets definition
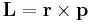
- där p är rörelsemängden.
Genom att derivera med avseende på tiden erhålls
Detta kan skrivas om med definitionen på rörelsemängd p = mv:
Den första termen i högerledet kan identifieras som kraft medan den andra blir noll till följd av kryssprodukten mellan två likriktade vektorer och därmed erhålls den sökta relationen.
Rörelse vid vridmoment
Då kraften F appliceras i en punkt som sammanfaller med masscentrum, uppstår inget vridmoment (τ = 0) och rörelsen är en translationsrörelse. Om en ända är fastsatt är rörelsen endast rotationsrörelse. Generellt ger vridmoment både en translations- och rotationsrörelse. Rörelsen ser olika ut beroende på rotationsaxelns läge. Exempelvis beskriver en punkt på ett roterande hjul är en rotationsrörelse betraktat från sidan medan den betraktad bakifrån beskriver en upp- och nerrörelse.
Associerade begrepp
Verkningslinjen (line of action) är en tänkt linje parallelt med kraften genom kraftens angreppspunkt.
Vridningsaxel är den axel runt vilken kroppen snurrar.
Kraftpar (force couple) är två symmetriska vridningar τ, en till höger och en likadan till vänster men med motsatt riktning. Kraftpar ger en ren rotationsrörelse.
Maskinlära
För att beräkna ett visst vridmoment hos en förbränningsmotor med hjälp av effekten och varvtalet används formeln: Nm = (kW * 9550) / varvtal