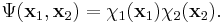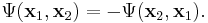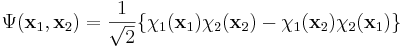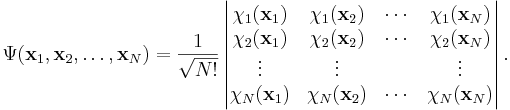Från Rilpedia

En slaterdeterminant (efter den Amerikanske fysikern John C. Slater) är inom kvantmekaniken ett uttryck för vågfunktionen av ett fler-fermion system, som har den inneboende egenskapen att den uppfyller pauliprincipen

Slaterdeterminanten härrör från att man ser på en vågfunktion som en hop elektroner. Vågfunktionen för varje enskild elektron kallas spin-orbital, 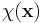, där 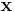indikerar positionen och spinnet hos elektronen.

Fallet med två partiklar

Det enklaste sättet att approximera vågfunktionen av ett flerkroppssystem är att ta produkten av väl valda en-elektron vågfunktioner av de individuella partiklarna. För fallet med två partiklar har vi

Detta uttryck används i Hartreemetoden som en ansatz för den molekylära vågfunktionen och är känd som en Hartreeprodukt. I vilket fall så är den inte tillfredsställande för fermioner som elektroner eftersom vågfunktionen inte är antisymmetrisk. En antisymmetrisk vågfunktion kan matematiskt beskrivas enligt:

Därför uppfyller alltså inte hartreeprodukten pauliprincipen. Detta problem kan man komma över genom att ta en linjärkombination av båda hartreeprodukterna:

där koefficienten är en normaliseringsfaktor. Denna vågfunktion är antisymmetrisk och skiljer inte längre mellan elektroner. Vidare går den också till noll om två av vågfunktionerna eller två av elektronerna är identiska. Detta är liktydigt med uppfyllandet av Pauliprincipen.

Generalization to the Slater determinant

The expression can be generalised to any number of fermions by writing it as a determinant. For an N-electron system, the Slater determinant is defined as

The linear combination of Hartree products for the two-particle case can clearly be seen as identical with the Slater determinant for N = 2. It can be seen that the use of (Slater) determinants assures an antisymmetrized function on the outset, symmetric functions are automatically rejected. In the same way, the use of Slater determinants assures the obeying of the Pauli principle; the determinant will vanish if any of the two spin-orbitals are identical, for this leads to two identical rows.

A single Slater determinant is used as an approximation to the electronic wavefunction in Hartree-Fock theory. In more accurate theories (such as configuration interaction and MCSCF), a linear combination of Slater determinants is needed.

The word "detor" was proposed by S. F. Boys to describe the Slater determinant of the general type ^[1].

References