Ultrafilter
Från Rilpedia
Inom matematiken, framförallt i mängdteori och modellteori är begreppet ultrafilter ett sätt att formalisera idén om en "stor" delmängd till en mängd M.
Innehåll |
Definition
Given en mängd M, så är ett filter F på M en icke-tom mängd av delmängder till M som satisfierar följnade villkor:
- Om
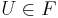 och
och 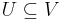 så
så 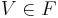
- Om
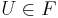 och
och 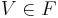 så
så 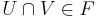
Ett filter F på M sägs vara ett ultrafilter om de är maximalt, dvs om följande villkor är uppfyllt:
- För varje
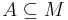 gäller
gäller 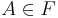 eller
eller 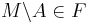
Ett ultrafilter F på M sägs vara principalt om det finns ett element 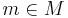 så att:
så att:
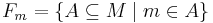 .
.
Existens
Principala ultrafilter på en mängd M existerar trivialt för varje 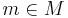 . Med hjälp av urvalsaxiomet kan man visa att det på varje oändlig mängd finns ett icke-principalt ultrafilter.
. Med hjälp av urvalsaxiomet kan man visa att det på varje oändlig mängd finns ett icke-principalt ultrafilter.
Exempel
De enda exempel på ultrafilter som konkret kan presenteras är de principala ultrafiltren, eftersom urvalsaxiomet krävs för att visa att andra ultrafilter existerar.
Användning
Ultrafilter används för att konstruera ultraprodukter, som används i mängdteori och modellteori



