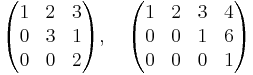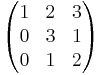Trappstegsmatris

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En trappstegsmatris (eller en matris på echelonform) är inom linjär algebra en benämning på en speciell matris.

En trappstegsmatris uppfyller:

  • Alla rader bestående av endast nollor är under alla rader som inte består av enbast nollor.
  • Pivotelementet i varje rad är strikt till höger om pivotelementet i raderna ovanför den.

Ibland läggs även följande villkor till:

  • Alla pivotelement är 1.

Vid Gausselimination fås en trappstegsmatris.

Exempel

Följande matriser är trappstegsmatriser (utan det tredje villkoret):

\begin{pmatrix} 1 & 2 & 3 \\ 0 & 3 & 1 \\ 0 & 0 & 2 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 & 3 & 4\\ 0 & 0 & 1 & 6\\ 0 & 0 & 0 & 1 \end{pmatrix}

Följande matris är inte en trappstegsmatris, eftersom pivotelementet i tredje raden inte är strikt till höger om pivotelementet i andra raden:

\begin{pmatrix} 1 & 2 & 3 \\ 0 & 3 & 1 \\ 0 & 1 & 2 \end{pmatrix}


Nuvola apps edu mathematics-p.svg Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Trappstegsmatris"
Personliga verktyg