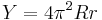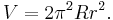Från Rilpedia

Torus är en matematisk kropp vars utseende i den vanliga tredimensionella varianten vanligen liknas vid en munk.

Den enklaste torusen inom matematiken är en 2-dimensionell "badringsformad" yta, en delmängd av 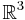, som brukar betecknas T ². Liksom sfären är den kompakt, medan den inte är enkelt sammanhängande. Dess Eulerkarakteristik är 0, dess genus är 1.

Exempel på parametrisering:

x = (1 + acos(ψ)) sin(φ)

y = (1 + asin(ψ)) sin(φ)

z = cos(φ)

(där 0<a<1)

Ett alternativt betraktelsesätt är att låta torusen vara en delmängd av 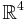. Parametriseringen blir då något enklare:

x = cos(ψ)

y = sin(ψ)

z = cos(φ)

t = sin(φ)

Detta eftersom torusen nu kan skrivas som en kartesisk produkt mellan två cirklar, d.v.s. T ² = S ¹ × S ¹. Denna version kallas även "den flata torusen", eftersom Riemannkrökningen här är konstant 0.

Generaliseringar kan ske på flera olika sätt. Dels genom att byta antalet dimensioner, vilket lättast beskrives lättast genom T ⁿ = S ¹ × S ¹ ... × S ¹ (denna torus är då en delmängd av R ²ⁿ), dels genom att göra flera hål. Om ringens tvärsnitt inte är en cirkel utan en annan sluten kurva brukar man tala om en toroid. Torusen kan då ses som ett speciellt slag av toroid.

Geometri

Om

R är avståndet från ringens centrum till själva torusens centrum, och

r är ringens radie

så följer för ytan och volymen för en cirkulär torus: