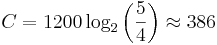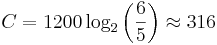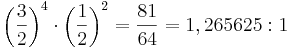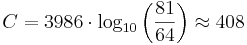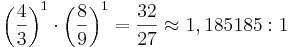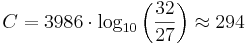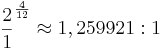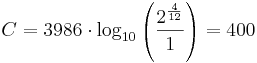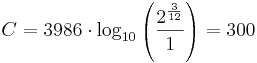Ters (musik)

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Diatoniska intervall
Spacer.gif
Ters
Stor (3S)
3 w.png
Lyssna (ljudfil)		 Liten (3L)
3 m.png
Lyssna (ljudfil)
Not: ljudfilerna stämmer inte alltid med
tonerna på bilderna, även om själva
intervallen är rätt.
Omvändning: Sext

Ters är ett musikaliskt intervall på två diatoniska steg, samt beteckning för den tredje tonen i en diatonisk skala. Ordet kommer av latinets tertius, ’tredje’.

Tersen finns liksom sexten i två varianter: stor och liten. Liten ters definierar molltonalitet, medan stor definierar dur. Dessutom finns flera möjligheter till intonation av tersen beroende på sammanhanget.

Innehåll

Härledning av intervallet

Ren stämning

Stor ters

Den stora tersen, durtersen, är ett mycket konsonant intervall som återfinns mellan 4:e och 5:e deltonen (samt mellan 8:e och 10:e) i den harmoniska deltonserien (4:5) och motsvarar frekvensförhållandet

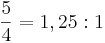\frac{5}{4}=1,25:1 (stor ters uppåt)
eller
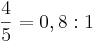\frac{4}{5}=0,8:1 (stor ters nedåt)

Centtalet för den stora rena tersen blir

C = 1200\log_2 \left(\frac{5}{4}\right)\approx{386}

Liten ters

Den lilla tersen, molltersen, kan vid första anblicken se ut att vara nästan lika konsonant som den stora tersen. Den hittas mellan 5:e och 6:e deltonen:

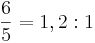\frac{6}{5}=1,2:1 (liten ters uppåt)
eller
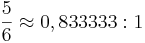\frac{5}{6}\approx{0,833333:1} (liten ters nedåt)

Men den stora tersen är konsonant mot grundtonen i tonarten (C-E i C-dur) medan den lilla tersen (E-G i C-dur) snarare är på väg att bilda ett e-mollackord i C-dur, vilket inte alls är lika konsonant.

Centtalet för den rena lilla tersen blir

C = 1200\log_2 \left(\frac{6}{5}\right)\approx{316}

Pythagoreisk stämning

Stor ters

I pythagoreisk stämning hittas den stora tersen genom att stapla 4 kvinter på varandra och sedan dra bort 2 oktaver:

\left(\frac{3}{2}\right)^{4}\cdot\left(\frac{1}{2}\right)^{2}=\frac{81}{64}={1,265625:1}

Centtalet för den stora pythagoreiska tersen blir

C = 3986\cdot\log_{10}\left(\frac{81}{64}\right)\approx{408}

Liten ters

Den lilla tersen fås genom att från en ren kvart (4:3) dra bort en pythagoreisk helton (8:9).

\left(\frac{4}{3}\right)^{1}\cdot\left(\frac{8}{9}\right)^{1}={\frac{32}{27}}\approx{1,185185:1}

Centtalet för den lilla pythagoreiska tersen blir

C = 3986\cdot\log_{10}\left(\frac{32}{27}\right)\approx{294}

Liksvävande temperatur

I liksvävande temperatur definieras alla intervall utifrån den liksvävande halvtonen.

Stor ters

Den stora tersen består av 4 liksvävande halvtoner och kan definieras som

\frac{2}{1}^\frac{4}{12}\approx{1,259921:1}

Centtalet för den stora liksvävande tersen blir

C = 3986\cdot\log_{10}\left(\frac{2^{\frac{4}{12}}}{1}\right) = 400

Liten ters

Den lilla tersen består av 3 liksvävande halvtoner och kan definieras som

\frac{2}{1}^\frac{3}{12}\approx{1,189207:1}

Centtalet för den stora liksvävande tersen blir

C = 3986\cdot\log_{10}\left(\frac{2^{\frac{3}{12}}}{1}\right) = 300

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Ters_(musik)"
Personliga verktyg