Skewes tal
Från Rilpedia
Texten från svenska Wikipedia
Skewes tal är det minsta heltal för vilket π(x) > li(x), där π(x) är antalet primtal mindre än x, och li(x) är den logaritmiska integralen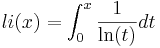 
.
Talet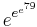 
(ungefär 
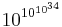) kallas Skewes första tal. Under förutsättning att Riemannhypotesen är sann så visade Skewe 1933 att detta är en övre uppskattning av det - än så länge okända tal - som idag kallas Skewes tal.
En uppskattning av Skewes tal i vilken Riemannhypotesen inte används visade han 1955 vara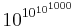 
, det så kallade Skewes andra tal.
H. J. J. te Riele lyckades 1987, utan att använda Riemannhypotesen, skärpa Skewes uppskattning kraftigt genom att visa att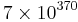 
är en övre gräns.
