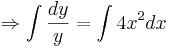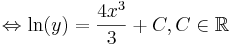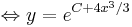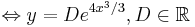Separabel differentialekvation

Texten från svenska Wikipedia

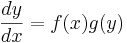
$\frac{dy}{dx} = f(x)g(y)$

kan variabelsepareras, vilket betyder att den allmänna formen ovan kan skrivas på följande sätt:

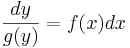$\frac{dy}{g(y)} = f(x)dx$ och sedan lösas med hjälp av integrering.

Exempel

Problem: $y' = 4 x 2 y$ .

$\Rightarrow \int \frac{dy}{y} = \int {4x^2dx}$

$\Leftrightarrow \ln(y) = {{4x^3} \over 3} + C, C \in \mathbb{R}$

$\Leftrightarrow y = e^{C+{4x^3}/ 3}$

$\Leftrightarrow y = De^{{4x^3}/ 3}, D \in \mathbb{R}$