Sadelpunkt
Från Rilpedia
Texten från svenska Wikipedia
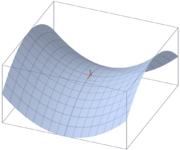
En sadelpunkt är inom matematik en punkt på en funktionskurva (eller funktionsyta) som är stationär men inte ett utgör ett lokalt extremum. Derivatan är alltid noll i en sadelpunkt, men omvändningen gäller inte i allmänhet. Om man däremot rör sig en aning bort från sadelpunkten kommer derivatan att vara positiv i vissa riktningar och negativ i andra riktningar. Tänk på en hästsadel, den är plan i punkten där man sitter men börjar luta neråt (dervatan är negativ) om man rör sig åt sidorna medan den lutar uppåt (positiv derivata) om man rör sig framåt eller bakåt. Icke-konstanta polynom kan ha sadelpunkter om de är av grad tre eller högre.
Exempel på en yta med en sadelpunkt är apsadeln.
