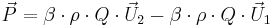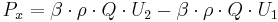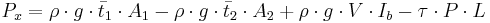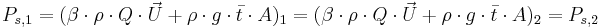Rörelsemängdekvationen
Från Rilpedia
Rörelsemängsekvationen behandlar rörelsemängd och är tillämplig vid kanalströmningen när strömningstillståndet övergår från subkritisk till superkritisk eller vice versa. Rörelsemängdekvationen är alltså tllämplig vid ett vattensprång.
där
P = Resultant för kontrollvolymen (kg*m/s2)
β = Korrektionsfaktor (-)
ρ = Densitet (kg/m3)
Q = Flöde (m3/s)
U = Hastighet (m/s)
Om man enbart tittar i strömriktningen (x-led), kan uttrycket skrivas
Om man studerar krafterna i strömningsriktningen, blir uttrycket:
där
Px = Resultant i xled för kontrollvolymen
ρ = Densitet (kg/m3)
g = Tyngdaccelerationen (9,82 m/s2)
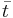= Avstånd mellan tyngdpunkt och vattenytan (-)
A = Tvärsnitsarea (m2)
V = Volym hos kontrollvolymen (m3)
Ib = Bottenlutning (-)
τ = Skjuvspänning (Pa)
P = Bottenbredd (m)
L = Längd (m)
Om bottenlutningen är liten och sektionerna ligger tätt gäller följande samband:
där
Ps = Specifik kraft
Den specifika kraften har sitt lägsta värde när Froudes tal blir 1 (kritisk strömning), alltså samtidigt som den specifika energin också når sitt lägsta värde. Det innebär att för varje superkritiskt djup finns det också ett subkritiskt djup med samma specifika kraft och energi.
Korrektionsfaktorn β
Inom rörströmningen brukar korrektionsfaktorn (β) sättas till 1 och sålunda försummas. Inom kanalströmningen blir däremot hastigheten så pass ojämt fördelad, att korrektionsfaktorn ej kan försummas.
| Typ av kanal | Min | Medel | Max |
|---|---|---|---|
| Rektangulär kanal | 1,03 | 1,05 | 1,07 |
| Naturlig strömfåra | 1,05 | 1,10 | 1,17 |
| Istäckta floder | 1,07 | 1,17 | 1,33 |
| Översvämmade dalgångar | 1,17 | 1,25 | 1,33 |
