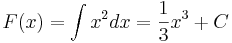Primitiv funktion
Från Rilpedia
| f(x) funktion |
F(x) primitiv funktion |
|---|---|
| k | kx + C |
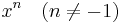 |
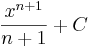 |
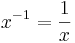 |
ln | x | + C |
| ex | ex + C |
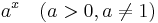 |
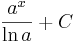 |
| sin(x) | − cos(x) + C |
| cos(x) | sin(x) + C |
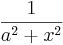 |
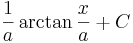 om om 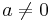 |
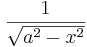 |
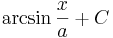 om a > 0 om a > 0 |
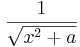 |
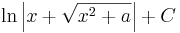 om om  |
| k och C är reella konstanter. | |
Primitiv funktion är ett begrepp inom matematisk analys.
En funktion F(x) är en primitiv funktion till f(x) om funktionen f är dess derivata, det vill säga om F '(x)=f(x). Ett alternativt uttryck för primitiv funktion är antiderivata, eller obestämd integral. Samma beteckning används som för integraler, fast utan några gränser. Primitiva funktioner används bland annat till algebraisk beräkning av integraler.
Eftersom derivatan av en konstant funktion är noll, finns det oändligt många primitiva funktioner till en funktion f. Om en primitiv funktion är F(x), så kan alla primitiva funktioner skrivas F(x) + C.
Exempel: Alla primitiva funktioner till
- f(x) = x2
kan skrivas
där dx betyder att integrering sker med avseende på variabeln x.
Märk att derivatan av den primitiva funktionen är lika med funktionen f.
Det är i allmänhet enklare att derivera än att göra motsatsen, men i gengäld så blir det således enkelt att kontrollera om en primitiv funktion är korrekt framtagen.
I tabellen till höger finns de vanligst använda primitiva funktionerna, även kallade standardprimitiver. Med dessa kan man komma långt, men ibland måste man ta till diverse olika knep för att omvanda en funktion till någon av dessa former.
Användbara räknelagar
För det första gäller samma linearitetsegenskaper som för derivata, dvs
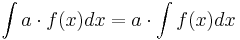 , förutsatt att konstanten a inte är noll, samt
, förutsatt att konstanten a inte är noll, samt
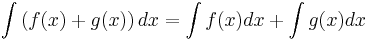 .
.
Vidare har man ofta användning av följade två satser,
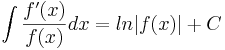 , samt
, samt
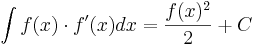 .
.
Den senare kan man säga är den omvända kedjeregeln, och man ser enkelt att båda dessa gäller genom att derivera högerledet.
Tycker man att dessa två steg är stora att ta, kan man göra variabelbytet f(x) = t, så omvandlas dessa till standardprimitiver som återfinns i tabellen till höger.
Dessa fyra regler, tillsammans med partialintegration och lämpliga variabelbyten utgör grunden för att analytiskt plocka fram primitiva funktioner.
Primitiva funktioner kan beräknas automatiskt med Risch algoritm.