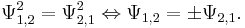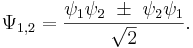Ourskiljbara partiklar
Från Rilpedia

Ourskiljbara partiklar eller identiska partiklar är i kvantmekaniken partiklar som inte kan urskiljas, inte ens i princip. Så har till exempel alla elektroner exakt samma massa, samma laddning och samma totala spinn. Alla elektroner med samma spinn är identiska, likaså alla protoner, alla 4He-atomer i grundtillståndet, och så vidare.
Även identiska partiklar kan man mäta och följa när de är på tillräckligt stort avstånd ifrån varandra. När dock avståndet blir mindre än de Broglie-våglängden, blir det enligt Heisenbergs obestämbarhetsprincip omöjligt att bestämma båda hastighet och position. Det går inte att skilja mellan till exempel de två banorna i skissen till höger. Det är till och med meningslöst att fråga vad som hände.
Ourskiljbarheten påverkar hur man räknar antalet olika tillstånd av ett system. Ourskiljbara partiklar vid höga densiteter följer därför inte statistisk mekanik enligt klassisk mekanik. Istället följer dessa partiklar Bose-Einstein-statistik om de är bosoner och de följer Paulis uteslutningsprincip och Fermi-Dirac-statistik om de är fermioner.
Symmetriska och antisymmetriska vågfunktioner
I en beskrivning av ett kvantmekaniskt system med två identiska partiklar, ska inte valet av indexordningen påverka mätningar. Vad som är mätbart beror på kvadraten av vågfunktionen:
Vågfunktionen måste alltså vara symmetrisk eller antisymmetrisk under utbyte av indices. Vågfunktionen för två identiska partiklar kan man skriva som produkt av en-partikelfunktioner:
Minustecknet gäller för fermioner (partiklar med halvtaligt spinn), plustecknet gäller för bosoner (partiklar med heltaligt spinn). Sambandet med partikelns intrinsiska rörelsemängdmoment kommer av att ett utbyte av koordinater kan beskrivas som en rotation över 180°.