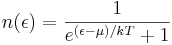Fermi-Dirac-statistik

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Fermi-Diracfunktionen för några olika temperaturer

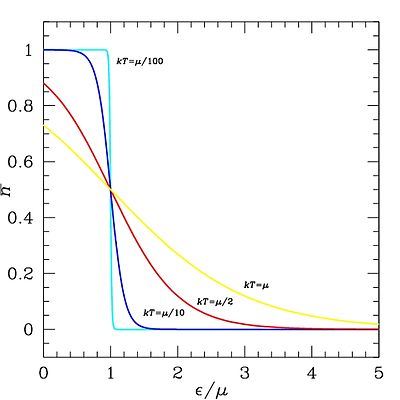
Fermi-Dirac-statistiken bestämmer sannolikhetsfördelningen för fermioners (till exempel elektroner i fasta kroppar tillhörande valens- och ledningsbanden) energitillstånd som funktion av temperaturen. Sannolikheten n(ε) för att en fermion befinner sig i ett kvanttillstånd med energin ε vid temperaturen T kan tecknas

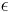n(\epsilon) = {1 \over {e^{(\epsilon - \mu)/kT} + 1}}

där

\ \epsilon är den aktuella energinivån
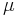\ \mu är den kemiska potentialen
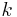\ k är Boltzmanns konstant
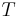\ T är temperaturen

Vid temperaturer nära absoluta nollpunkten är för varje energinivå 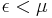\ \epsilon < \mu sannolikheten nära 1 för att energinivån är besatt. Vid låga temperaturer är 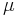\ \mu lika med Ferminivån.


Cat silhouette.svg Denna artikel om kvantfysik eller subatomär fysik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Fermi-Dirac-statistik"
Personliga verktyg