Ouppnåeliga kardinaltal

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett kardinaltal κ sägs vara ouppnåeligt om följande gäller:

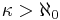
  • \kappa >\aleph_0
  • κ kan inte skrivas som en union av färre än κ mängder med kardinalitet mindre än κ
  • om η < κ så 2η < κ

Om κ är ouppnåeligt så är Vκ en modell till ZFC. Detta innebär att existensen av ouppnåeliga kardinaltal inte följer ur ZFC, ty då hade teorin bevisat sin egen konsistens vilket Gödels andra ofullständighetssats inte tillåter.

Hämtad från "https://sv.rilpedia.org/wiki/Ouppn%C3%A5eliga_kardinaltal"
Personliga verktyg