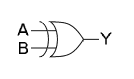Från Rilpedia
 Texten från svenska Wikipedia
Texten från svenska Wikipedia
En logisk disjunktion förenar två påståenden till ett nytt påstående med betydelsen att något av påståendena gäller. Disjunktion motsvaras i det svenska språket av ordet "eller" i två betydelser. När man säger "Du kan få en kopp kaffe eller te om du vill" menar man vanligen antingen en kopp kaffe eller en kopp te, inte både och. När man säger att "det är dåligt väder när det regnar eller blåser" menar man vanligen att det är dåligt väder även när det regnar och blåser. I logiska sammanhang skiljs dessa betydelser åt som en exklusiv disjunktion (antingen p eller q men ej båda) och en inklusiv disjunktion (p eller q eller båda).
Representation
Inklusiv disjunktion betecknas vanligen med ∨ och exklusiv disjunktion med xor eller ∨. I boolesk algebra betecknas inklusiv disjunktion med + och exklusiv disjunktion med ⊕ som där motsvarar speciella varianter av addition. En inklusiv disjunktion mellan de två påståendena p och q skrivs som p ∨ q och en exklusiv disjunktion som p xor q.
Mening, sanningsfunktion och sanningstabell
Disjunktionens egenskaper beskrivs i klassisk logik som en funktion – en sanningsfunktion – av de ingående påståendenas sanning. Detta definierar disjunktionens mening och kan beskrivas med en sanningstabell (s = sann, f = falsk):
Inklusiv disjunktion
| p |
q |
p ∨ q |
| s |
s |
s |
| s |
f |
s |
| f |
s |
s |
| f |
f |
f |
|
Exklusiv disjunktion
| p |
q |
p xor q |
| s |
s |
f |
| s |
f |
s |
| f |
s |
s |
| f |
f |
f |
|
Boolesk algebra
I boolesk algebra beskrivs disjunktion i matematiska termer som sanningsfunktion enligt:
(p ∨ q) = p + q
(p xor q) = p ⊕ q
Med talen 1 för sann och 0 för falsk och de booleska specialreglerna 1+1=1 och 1⊕1=0 motsvarar funktionernas egenskaper följande tabeller:
Inklusiv disjunktion
| p |
q |
p ∨ q |
| 1 |
1 |
1 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
|
Exklusiv disjunktion
| p |
q |
p xor q |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
|
I en variant av boolesk algebra utan specialregler för de matematiska operationerna * och + beskrivs dessa disjunktioner med sanningsfunktionerna
(p∨q) = p + q - p*q
(p xor q) = p + q - 2*p*q
med egenskaper enligt tabellen
Inklusiv disjunktion
| p |
q |
p + q - p*q |
| 1 |
1 |
1 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
|
Exklusiv disjunktion
| p |
q |
p + q - 2*p*q |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
|
Tekniska lösningar
I elektriska kretsar, pneumatik, hydraulik, mekanik etc kan funktioner som motsvarar disjunktioner realiseras, som i kombination med andra logiska funktioner kan byggas ihop till komplex funktionalitet. Några exempel:
Parallellkoppling
Om till exempel två parallellkopplade brytare seriekopplas med en lampa måste båda brytarna vara från för att lampan ska vara släckt; i annat fall tänds lampan. Detta realiserar en inklusiv disjunktion.

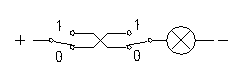
Trappomkastare
En (korsad) trappomkastare realiserar en exklusiv disjunktion (se bild).
OR-grind och XOR-grind
I digitaltekniken realiseras samma funktioner med logiska byggblock, OR-grind respektive XOR-grind. "Värdena" är här signalena "hög" och "låg" som motsvarar bestämda spänningsintervall. Dessa betecknas vanligen med H = high och L = low.

(IEC symbol)
|
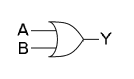
(US symbol)
|
Inklusiv disjunktion
| A |
B |
A OR B |
| H |
H |
H |
| H |
L |
H |
| L |
H |
H |
| L |
L |
L |
|
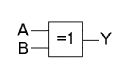
(IEC symbol)
|
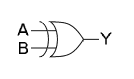
(US symbol)
|
Exklusiv disjunktion
| A |
B |
A XOR B |
| H |
H |
L |
| H |
L |
H |
| L |
H |
H |
| L |
L |
L |
|