Minsta gemensamma multipel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Minsta gemensamma multipel, begrepp inom matematik.

En multipel till ett tal a är talet multiplicerat med något positivt heltal; till exempel så har vi följande multiplar till 5:

5, 10, 15, 20, 25.

En gemensam multipel till två heltal är en tal som är en multipel av vart och ett av talen.

Multiplar av 6: 6,12,18,24,30,36,42,48,54...

Multiplar av 8: 8,16,24,32,40,48,56...

Gemensamma multiplar av 6 och 8: 24,48,...

Den minsta gemensamma multipeln till 6 och 8 är således 24.

Tillämpning vid bråkberäkning

Begreppet används till exempel om en summa eller differens av två bråk ska beräknas. Den minsta gemensamma multipeln av nämnarna är den nämnare, man kommer få ut i ett första svar (som sedan kanske kan förkortas...)

Till exempel:

Uppgift
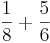
Beräkna \frac{1}{8}+\frac{5}{6}
Lösning
  1. den minsta gemensamma multipeln av 6 och 8 är 24
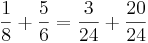
  2. förläng båda bråken så att man får nämnaren 24 (som beräknat ovan): det första bråket måste då förlängas med 3, och det andra med 4. Uppgiften är nu i läget \frac{1}{8}+\frac{5}{6} = \frac{3}{24} + \frac{20}{24}
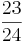  3. Talen har nu samma nämnare, alltså är summan \frac{23}{24}.

I praktiken kallas just denna tillämpning på bråktal av "minsta gemensamma multipler" för minsta gemensamma nämnare

Se även


Nuvola apps edu mathematics-p.svg Denna artikel om algebra är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Minsta_gemensamma_multipel"
Personliga verktyg