Från Rilpedia

Spel eller huvudbry där man söker sig fram till lösningen på ett problem genom att logiskt pröva de möjligheter och – lika viktigt – omöjligheter som finns. Ett logikspel skall inte kräva att man gissar sig fram till lösningen.

Ett välkonstruerat problem i ett logikspel har endast en lösning.

Innehåll 1 Nyttan med logikspel 2 Historia 3 Exempel 4 Verbala logikspel 5 De två barnen 6 Externa länkar

Nyttan med logikspel

Logikspel använder ofta siffror men i många fall, som i Sudoku och Hitori, kan dessa bytas mot bilder eller andra symboler. Detta gör det möjligt att konstruera enkla problem även för små barn som ännu inte har lärt sig siffrorna.

Man kan förmoda att logikspel utvecklar individens förmåga till logiskt och systematiskt tänkande, vilket i så fall skulle ge dem ett pedagogiskt värde men även göra dem värdefulla för äldre som önskar hålla hjärnan i trim.

Historia

Logikspel har en lång tradition i länder som Storbritannien och framför allt Japan. I Sverige finns inte samma tradition, men på senare tid har intresset för Sudoku exploderat och medfört att ett stort antal tidskrifter och böcker om detta logikspel publicerats.

Exempel

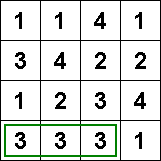
I ett rutnät med siffror skall så få rutor som möjligt färgas så att följande villkor uppfylls:

1. Ingen rad eller kolumn får innehålla samma ofärgade siffra mer än en gång.
2. Inga intilliggande rutor får färgas.
3. Det skall finnas en sammanhängande väg genom alla de ofärgade rutorna.
   

I den nedersta raden finns tre treor intill varandra. Om någon av de yttre treorna lämnas ofärgad, måste båda de andra färgas för att regel 1 skall uppfyllas.

Detta skulle leda till att två intilliggande rutor färgades, vilket bryter mot regel 2.

Logisk slutsats: Båda de yttre treorna måste färgas.

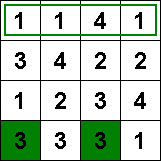
I den översta raden finns tre ettor, uppdelade på två grupper. Kan den ensamma ettan till höger lämnas ofärgad?

Detta skulle kräva att båda de återstående ettorna färgades, vilket skulle bryta mot regel 2.

Logisk slutsats: Den ensamma ettan måste färgas.

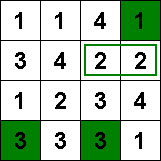
I andra raden finns två tvåor. Kan den högra färgas?

Detta skulle ge två intilliggande färgade rutor, vilket bryter mot regel 2.

Logisk slutsats: Den vänstra tvåan måste färgas.

I översta raden finns två ettor. Kan den högra färgas?

Detta skulle stänga in fyran i raden och bryta mot regel 3.

Logisk slutsats: Den vänstra ettan måste färgas.

Rutnätet motsvarar nu alla reglerna. Ingen siffra förekommer mer än en gång i en rad eller kolumn, inga intilliggande rutor är färgade och det finns en sammanhängande, ofärgad väg genom de ofärgade rutorna.

Typiska logikspel är Sudoku, Hitori och Loop the Loop. Även Extrem sudoku och Kakuro är logikspel, men eftersom dessa bygger på räknande kan siffrorna inte ersättas av andra symboler.

Verbala logikspel

Alla logikspel använder inte siffror eller liknande symboler. En del utnyttjar i stället rent verbala ledtrådar som när de tolkas på det logiskt riktiga sättet ger svaret på problemet. Ett typiskt sådant spel är Einsteins gåta.

De två barnen

Här följer ett exempel på en annan typ av logikspel, eller logiska gåtor. De är dock egentligen inga spel, utan handlar snarare om att resonera logiskt.

Två gamla klasskamrater träffas för första gången sedan skolan slutade tio år tidigare.

Den ena frågar den andra: Hur många barn har du?
Svar: Två.
Fråga: Hur gamla är de?
Svar: Det ena är fyra och det andra två år.
Fråga: Är något av dem en flicka?
Svar: Ja.

Hur stor är sannolikheten för att även det andra barnet är en flicka? (Vi förutsätter att hälften av alla barn som föds är flickor.)

Det intuitivt självklara svaret är att sannolikheten är 1:2 eller 50 procent, eftersom det bara finns två möjligheter och eftersom det ena barnets kön inte borde påverka det andra barnets. Men stämmer det?

Om en mamma har fött två barn, kan könsfördelningen mellan barnen vara någon av följande:

1. Det första barnet är en pojke och det andra barnet är en pojke.
2. Det första barnet är pojke och det andra barnet är en flicka.
3. Det första barnet är en flicka och det andra barnet är en pojke.
4. Det första barnet är en flicka och det andra barnet är en flicka.

Eftersom vi vet att minst det ena barnet är en flicka, kan vi stryka möjlighet 1. Vi vet däremot inte om det är det äldsta eller det yngsta barnet som är en flicka. Kvar finns då tre möjligheter och alla tre är lika sannolika. En av dessa tre möjligheter säger att det första barnet är en flicka och det andra barnet är en flicka. Sannolikheten för att båda barnen är flickor blir därför 1:3 eller ungefär 33 procent.

Om vi hade vetat att det äldsta barnet var en flicka, hade endast möjligheterna 3 och 4 återstått, och sannolikheten för att det andra barnet också är flicka skulle öka till 1:2 eller 50 procent. Detsamma gäller om vi hade vetat att det yngsta barnet var en flicka – då hade möjligheterna 2 och 4 återstått.

Men stämmer nu detta? Kan vi – när vi redan vet att det ena barnet är en flicka – anse att möjligheterna enligt ovan existerar? Eller är det följande möjligheter som gäller:

1. Det ena barnet är en flicka och det andra en pojke.
2. Det ena barnet är en flicka och det andra är också en flicka.

I så fall är sannolikheten för båda lika stor och sannolikheten för att båda barnen är flickor blir således 1:2.

Externa länkar

http://www.edcollins.com/logic/ Engelskspråkig webbplats med ett trettiotal logiska problem av typen "De två barnen"