Sudoku
Från Rilpedia
Sudoku (数独, sūdoku), ibland kallat su doku, är ett logikspel som går ut på att man ska placera ut siffror i ett rutmönster. Det klassiska, ursprungliga rutmönstret består av 3 × 3 rutor (”lådor”) som i sin tur består av 3 × 3 rutor. Det gäller att placera in siffrorna 1 till 9 på ett sådant sätt att varje vågrät rad, lodrät rad och låda på 3 × 3 rutor innehåller varje siffra exakt en gång.
Ett sudoku har minst 17 siffror utplacerade från början, och för att det ska anses som äkta får det bara ha en lösning.
Innehåll |
Historia
Sudoku uppfanns i USA i slutet av 1970-talet, men vann då ingen popularitet. På 1980-talet introducerades det i Japan där det också fick sitt namn, ursprungligen suuji wa dokushin ni kaguru ("en siffra som måste förbli utan par"), vilket kortades till su doku ("ensam siffra"). Det fick en ny blomstringsperiod i Storbritannien 2005, till stor del därför att nyzeeländaren Wayne Gould konstruerade ett datorprogram som snabbt genererar nya pussel.
Den 2 juni 2005 började Sydsvenska Dagbladet och Svenska Dagbladet som första svenska tidningar publicera ett sudoku om dagen. I dag har de flesta svenska tidningar ett dagligt sudoku och det finns en rad specialtidskrifter som främst ägnar sig åt sudoku. Dessutom finns ett relativt stort antal sudokuböcker.
Populariteten i Japan och Storbritannien kan förklaras av att båda länderna har en mycket lång tradition för logiska spel, men det har ännu inte framkommit någon sociologisk förklaring till att sudoku blivit en sådan succé i Sverige.
Varianter
Det finns i dag ett stort antal varianter på sudoku. En av dem är Godoku, där siffrorna ersatts av bokstäver. En annan är samurajsudoku, som består av flera sudokuplaner där varje enskild plan har en låda gemensam med någon av de andra planerna. En tredje variant, som kan vara betydligt svårare än vanligt sudoku, är extrem sudoku.
Extremsudoku
Extremsudoku (engelska: killer sudoku eller sumdoku; japanska: samunamupure) är en svårare variant av sudoku. Till skillnad från ett vanligt sudoku ges inga hjälpsiffror alls från början. I stället är hela sudokuplanen indelad i grupper som markeras av streckade linjer. I varje grupps övre vänstra hörn anges den summa som siffrorna i gruppen skall ge.
I övrigt gäller de normala sudokureglerna: Varje rad, kolumn och block skall innehålla siffrorna 1-9 exakt en gång. För extrem sudoku gäller dessutom att en grupp inte får innehålla samma siffra mer än en gång.
Några lösningsmetoder
- Börja med att leta efter block med en enda grupp där en enda siffra går över blockgränsen. Eftersom totalsumman i varje block skall vara 45, blir det lätt att upptäcka vilken siffra som skall stå i den gränsöverskridande rutan. I bilden ser vi att det nedersta blockets grupper ger totalsumman 41. Därför måste den ensamma rutan från blocket ovanför innehålla en 4. Därmed blir det även klart att det övre blockets övre vänstra ruta måste innehålla 5.
- Sök efter gruppsummor där gruppen måste innehålla bestämda siffror. Exempel på detta: En grupp med summan 3 måste bestå av 1 och 2, en grupp med summan 4 måste bestå av 1 och 3, en grupp med summan 23 måste bestå av 6, 8 och 9. Undersök om dessa "tvingande siffror" utesluter förekomsten av andra "tvingande siffror" i samma block, rad eller kolumn. I bilden ser vi att det övre blockets vänstra kolumn innehåller en grupp med summan 5. Denna summa måste bildas av 1 och 4 eller av 2 och 3. Eftersom gruppen redan innehåller 1, måste 5-gruppen bestå av 2 och 3.
- Sök efter grupper med lika totalsumma och lika antal rutor inom ett och samma block. I bilden ser vi att det nedersta blocket innehåller två 2-rutorsgrupper med totalsumman 14. 14 på två rutor kan bara bestå av 5 och 9 eller 6 och 8. Eftersom det övre blockets översta vänstra ruta måste innehålla 5, kan den lodräta 14-gruppen i det nedre blocket bara bestå av 6 och 8. Detta i sin tur gör att den vågräta 14-gruppen måste bestå av 5 och 9. Eftersom 5 redan finns i den vänstra kolumnen, måste 5 i den vågräta 14-gruppen stå i den högra rutan.
- Man har mycket stor hjälp av att lära sig de sifferkombinationer som med olika rutantal blir de enda möjliga för att åstadkomma bestämda gruppsummor.
- Glöm inte att de vanliga sudokureglerna gäller. Du kan därför dessutom använda alla de normala lösningsmetoderna.
Samurajsudoku
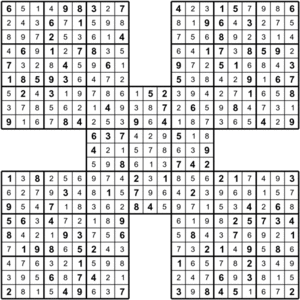
Samurajsudoku, eller familjesudoku, är en variant av sudoku som under år 2005 spred sig explosionsartat från Japan över världen. Den här varianten kännetecknas av flera överlappande sudoku, ihoplagda så att varje plan har minst ett hörnblock gemensamt med ett hörnblock i en annan plan. Ofta saknas givna siffror helt och hållet i de för flera planer gemensamma blocken.
Varje enskild sudokuplan i ett samurajsudoku består av 9 x 9 rutor, uppdelade i 3 x 3 block med 9 rutor i varje. För var och en av planerna gäller de normala sudokureglerna: Man skall placera siffrorna 1 till 9 i de tomma rutorna. Varje rad, spalt och block skall innehålla alla nio siffrorna exakt en gång.
Den vanligaste varianten av samurajsudoku består av fem planer, i Japan kallat Gattai 5 sudoku ("fem kopplade sudoku"). I Japan är det dock inte ovanligt med tjugo eller fler hopkopplade planer.
Godoku
Godoku är samma sak som sudoku fast med skillnaden att i godoku används bokstäver i stället för siffror. I ett godoku gömmer det sig ofta ett ord, men det är inget krav för att det ska kallas ett godoku.
Taktik
Det finns i grunden två frågor att använda för att lösa sudokut:
- I vilken ruta ska denna siffra sitta?
- Vilken siffra ska sitta i denna ruta?
Med uteslutningsmetoden kan dessa frågor itereras runt på alla 9 lådor, rader och kolumner, och till sist har man löst pusslet.
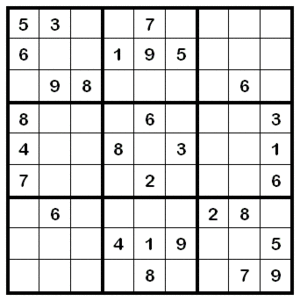
Ett snabbt sätt att få några siffror på plats är att utgå från en siffras förekomst i två av tre närliggande 3 × 3-lådor. I bildexemplet kan man se att siffran 5 finns i två av de tre lådorna överst. Eftersom den också ska finnas i översta lådan till höger, så kan man i de vågräta raderna se att vågrät rad 1 och 2 är upptagna, och att 5 därför ska finnas i vågrät rad 3 för lådan till höger. Mittpositionen är upptagen av siffra 6, raden till höger är upptagen av siffran 5 i lådan längst ner till höger, vilket innebär att 5 ska placeras på plats vågrät 3, lodrät 7! Med denna teknik kan man gå igenom alla siffror och ofta komma en bra bit på vägen. Oftast tar det stopp efter ett tag, och då rekommenderas att granska täta vågräta rader, lodräta rader eller lådor, för att se om man med uteslutningsmetoden kan placera ut återstående siffror.
Om man verkligen kör fast, kan man behöva räkna på längre logiska sekvenser som leder fram till en inkonsekvens, vilket gör att det andra alternativet är det riktiga. Då krävs ofta att man noterar vilka siffror som är möjliga i varje ruta. För svåra sudoku måste man börja med att utesluta att en viss siffra kan finnas på en viss plats, och efter några sådana uteslutningar kan man komma fram till beroenden som leder till en slutsats om en viss siffra på en viss position.
Tips
Sätten att lösa sudokun är många, så det gäller att hitta den metod som passar lösaren bäst. I svårare sudokun måste man använda flera olika metoder för att komma fram till lösningen. Nedan presenteras en del av de grundläggande metoderna.
- Enda siffra: Om en ruta bara kan innehålla en enda siffra, sätter man ut den.
- Enda plats: Om en siffra bara kan finnas på en enda plats i en rad, kolumn eller låda, sätter man ut den.
- Par: Om två siffror bara kan finnas i två rutor i en rad, kolumn eller låda, kan ingen annan siffra finnas i dessa rutor. Alla andra kandidater kan då strykas ur dessa rutor.
- Tripplar: Här gäller samma sak som för par, men med tre siffror respektive rutor.
- Enda rad/kolumn: Om två lådor med gemensamma rader eller kolumner måste ha en och samma siffra på två av raderna eller kolumnerna, måste den tredje lådan använda den återstående raden eller kolumnen. Den här metoden blir särskilt användbar när alla tre rutorna på en rad eller kolumn inom en låda är fyllda.
- Pricksystemet: för att systematiskt hitta den entydiga lösningen kan det hjälpa att i varje ruta sätta en prick som motsvarar en siffra från 1-9. Tänk dig att varje ruta delas in i nio rutor, dvs tre rader och tre kolumner. Låt siffra 1 motsvara en prick i det övre vänstra hörnet, siffra 2 en prick i den översta raden kolumn två.....siffra 5 i mitten...etc. Utifrån detta kan man sedan systematisk hitta lösningen. Kan behövas i senare skeden i svårare sudoku.
- Kandidater: Detsamma som pricksystemet, men sätt ut små siffror med blyerts längs rutans överkant i stället.
- X-flygel: Om en kandidat förekommer exakt två gånger i en och samma rad eller kolumn, och samma kandidat förekommer exakt två gånger även i en annan rad eller kolumn, samt på samma rad/kolumn som den första kandidaten, måste siffran stå på någon av dessa platser. Alla andra förekomster av denna kandidat i samma rader, kolumner eller lådor kan därför strykas.
Externa länkar
(engelska)
(engelska)
- Sudoku Puzzle Generator and Solver, sudokugenerator och -lösare för GNU R
(engelska)