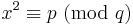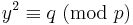Kvadratiska reciprocitetssatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Den kvadratiska reciprocitetssatsen, förmodad av Euler och Legendre och först bevisad av Gauss, kopplar samman lösbarheten av två relaterade kvadratiska kongruenser inom modulär aritmetik. Satsen gör det möjligt att bestämma lösbarheten för alla kvadratiska kongruenser inom modulär aritmetik.

Antag att p och q är två olika udda primtal. Om åtminstone en av dem är kongruent 1 modulo 4 så har kongruensen

x^2\equiv p\ ({\rm mod}\ q)

en lösning x om och endast om kongruensen

y^2\equiv q\ ({\rm mod}\ p)

har en lösning y. (De två lösningarna är i allmänhet olika.) Om å andra sidan båda primtalen är kongruenta 3 modulo 4 så har kongruensen

x^2\equiv p\ ({\rm mod}\ q)

en lösning x om och endast om kongruensen

y^2\equiv q\ ({\rm mod}\ p)

saknar lösning.

Om man använder Legendresymbolen 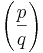\left(\frac{p}{q}\right), så kan detta sammanfattas som

\left( \frac{p}{q} \right)\cdot \left( \frac{q}{p} \right) =(-1)^{(p-1)/2\cdot(q-1)/2}.

Lemmermeyer samlar år 2000 i en bok 196 olika publicerade bevis för den kvadratiska reciprocitetssatsen.

Det finns en kubisk reciprocitetssats och andra högre reciprocetetssatser.


Question book-4.svg
 Den här artikeln saknar källhänvisningar. Förbättra gärna artikeln genom att lägga till pålitliga källor (helst fotnoter). Material som inte kan verifieras kan ifrågasättas eller tas bort. (maj 2009)
Hämtad från "https://sv.rilpedia.org/wiki/Kvadratiska_reciprocitetssatsen"
Personliga verktyg