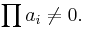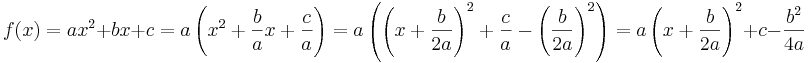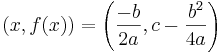Andragradsfunktion
Från Rilpedia
En andragradsfunktion är en polynomfunktion av andra graden.
Andragradsfunktioner av en variabel
Grafen till en andragradsfunktion av en variabel är en parabel. Begreppet andragradskurva används ibland felaktigt synonymt med grafen till en andragradsfunktion. Grafen till en andragradsfunktion är en andragradskurva, men en andragradskurva måste inte vara grafen till en andragradsfunktion.
Om a > 0 har funktionen en minimipunkt och går mot 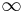 då x går mot
då x går mot 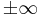
Om a < 0 har funktionen en maximipunkt och går mot 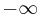 då x går mot
då x går mot 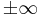
Max/min-punkten kallas funktionsgrafens vertex, och den lodräta linjen därigenom kallas grafens symmetrilinje.
Genom kvadratkomplettering kan man skriva om
Utifrån det kan man utläsa att funktionens max/min uppnås då kvadraten är 0, dvs
Dessutom visar ekvationen att graferna till alla andragradsfunktioner av en variabel är likformiga
Andragradsfunktioner i fler dimensioner
Andragradsfunktioner kan generellt skrivas på formen
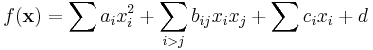 , där
, där 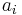 ,
, 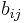 ,
, 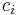 och
och 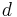 är konstanter och
är konstanter och