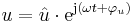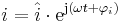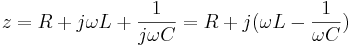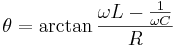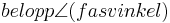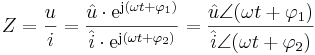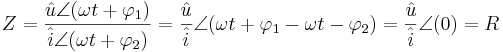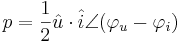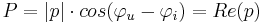jω-metoden
Från Rilpedia
jω-metoden, j-omega-metoden, används för att beräkna strömmar och spänningar i växelströmskretsar.
Genom att representera impedanserna för spolar (induktanser) och kondensatorer (kapacitanser) med komplexa tal kan man tillämpa den relativt enkla likströmsteorin på kretsar med växelspänningar av konstant frekvens (till exempel 50 Hz nätspänning).
Vid 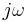 -metoden används symbolen
-metoden används symbolen 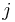 för den imaginära enheten. Orsaken är att symbolen
för den imaginära enheten. Orsaken är att symbolen 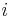 inom elektrotekniken ofta används för att beteckna strömmar.
inom elektrotekniken ofta används för att beteckna strömmar. 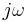 -metoden grundar sig i huvudsak på följande:
-metoden grundar sig i huvudsak på följande:
- Växelströms/växelspänningsförloppen antas vara sinusformiga
- Växelströms/växelspänningsförloppens frekvenser
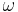 (radianer per sekund) antas vara konstanta. De induktiva och kapacitiva egenskaperna hos en krets är därmed konstanta (varierar ej med växelförloppens frekvenser).
(radianer per sekund) antas vara konstanta. De induktiva och kapacitiva egenskaperna hos en krets är därmed konstanta (varierar ej med växelförloppens frekvenser). - En induktans ger en fasvridning av +90 grader. För ett komplext tal motsvaras detta av en multiplikation med imaginära enheten. Den komplexa induktiva impedansen kan då skrivas som
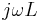
- En kapacitans ger en fasvridning av -90 grader. För ett komplext tal motsvaras detta av en division med imaginära enheten. Den komplexa kapacitiva impedansen kan därför skrivas
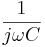
- En resistans ger en fasvridning av 0 grader vilket motsvarar ett komplext tal med imaginärdelen lika med noll och kan skrivas som
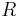
Även strömmar och spänningar skrivs som komplexa tal, till exempel som
På grund av de komplexa talens egenskaper kan således ett komplext tal beskriva både belopp och fasvinkel för en impedans, ström eller spänning. Det går därmed att beräkna växelstorheter enligt de vanliga grundläggande reglerna och samtidigt implicit behandla både belopp och fas.
Exempel
Impedansen för en seriekoppling av tre komponenter med resistans, induktans respektive kapacitans kan skrivas som ett komplext tal enligt
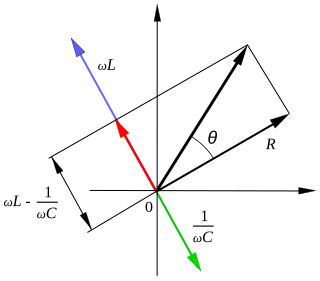
Av visardiagrammet till höger framgår att den resulterande fasvridningen för de seriekopplade impedanserna är
vilket är samma värde som argumentet för den komplexa impedansen 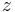 .
.
Det framgår också att resultantens belopp i visardiagrammet är lika med 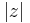 .
.
I visardiagrammet används en riktfas (visaren för R, den resistiva komponenten) som fasreferens. Riktfasen har ofta samma fas som strömmen genom resistorn om sådan förekommer i kretsen.
Ofta används en särskild notation för de komplexa impedanserna, strömmarna och spänningarna:
Med den notationen kan till exempel Ohms lag skrivas
Vi ser av uttrycket för 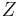 att om
att om 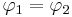 , det vill säga om
, det vill säga om 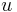 och
och 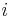 är i fas, att
är i fas, att
Givet att
och med 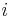 som riktfas, kan vi skriva den utvecklade effekten som
som riktfas, kan vi skriva den utvecklade effekten som
där  är fasdifferensen mellan spänningen och strömmen och där faktorn
är fasdifferensen mellan spänningen och strömmen och där faktorn 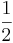 beror på övergång till effektivvärden för
beror på övergång till effektivvärden för 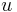 och
och 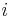 . Den reella effekten erhålls genom projektion av resultanten på den resistiva komponenten
. Den reella effekten erhålls genom projektion av resultanten på den resistiva komponenten 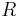 som kan antas ha samma riktning som
som kan antas ha samma riktning som 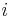 :
:
det vill säga, 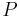 är
är 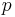 's reella del.
's reella del.
Historik
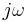 -metoden går tillbaka till Arthur Edwin Kennelly (1861-1939), som 1893 presenterade ett arbete om "Impedance" vid det amerikanska ingenjörsinstitutet American Institute of Electrical Engineers, AIEE.
-metoden går tillbaka till Arthur Edwin Kennelly (1861-1939), som 1893 presenterade ett arbete om "Impedance" vid det amerikanska ingenjörsinstitutet American Institute of Electrical Engineers, AIEE.