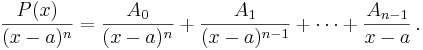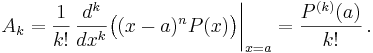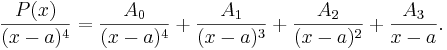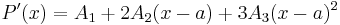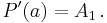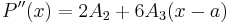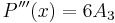Heavisides expansionsregel
Från Rilpedia
Heavisides expansionsregel är inom matematiken en metod för att bestämma koefficienter vid partialbråksuppdelning, uppkallad efter Oliver Heaviside.
Metoden
Heavisides expansionsregel kan användas då faktorerna i nämnaren har formen 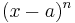 , och då täljarens gradtal är strikt mindre än nämnarens. Om så inte är fallet kan polynomdivision utföras.
, och då täljarens gradtal är strikt mindre än nämnarens. Om så inte är fallet kan polynomdivision utföras.
Den vanliga ansatsen för ett sådant bråk är
För att bestämma den första koefficienten sätts 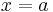 in i täljaren. För att bestämma den andra koefficienten sätts
in i täljaren. För att bestämma den andra koefficienten sätts 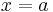 in i
in i 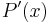 , det vill säga täljarens derivata. Generellt gäller, för den k:te koefficienten:
, det vill säga täljarens derivata. Generellt gäller, för den k:te koefficienten:
Ett exempel
Betrakta ett bråk där nämnarens gradtal är fyra. För ett sådant bråk gäller ansatsen
Börja med att multiplicera båda led med (x − a)4
-
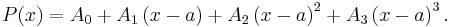
(1)
Koefficienterna A0, A1, A2 och A3 bestäms sedan genom att successivt derivera båda led i denna identitet och sätta in x = a.
- Sätts x = a in i båda led i (1) fås direkt att
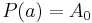 .
.
- För att få fram A1 deriveras först båda leden i (1) med avseende på x
- Koefficienten A2 bestäms genom att derivera båda led i (1) ytterligare en gång
- Till slut, för att få A3 deriveras ekvation (1) en sista gång