Från Rilpedia

Inom matematik sägs en funktion f på 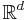vara Hölderkontinuerlig eller uppfylla ett Höldervillkor om det finns konstanter C och α så att

Detta kan generaliseras till funktioner mellan metriska rum; om g är en funktion från metriska rummet (X,d_X) till (Y,d_Y) så är g Hölderkontinuerlig om det finns konstanter C och α så att:

Speciellt, om α = 1 är funktionen Lipschitzkontinuerlig och om α = 0 är funktionen en begränsad funktion.

Inom funktionalanalys studeras Hölderrum i syfte att lösa partiella differentialekvationer. Hölderrummet C^n,α(Ω), där Ω är en öppen delmängd till något euklidiskt rum och n något naturligt tal, består av funktioner som har derivator upp till ordning n så att n:te ordningens partiella derivatorer är Hölderkontinuerliga med exponent α, där 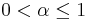.