Härledningssystem

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett härledningssystem är ett formellt system som specificerar hur bevisföring i en given kontext går till. Ett sådant system kan bestå av enbart axiom eller axiom och härledningsregler.

Ett klassiskt exempel på ett härledningssystem är David Hilberts system för satslogik, vilket består av tre axiom och en regel:

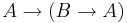
(Axiom 1) A \to (B \to A)
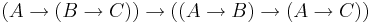
(Axiom 2) (A \to (B \to C)) \to ((A \to B) \to (A \to C))
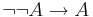
(Axiom 3) \lnot \lnot A \to A
(Regel (Modus ponens)) Från 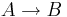A \to B och A får B härledas.

För satslogik såväl som för predikatlogik finns en mängd olika härledningssystem av olika karaktär. En del är praktiskt användbara, på så vis att de innehåller intuitiva härledningsregler medan andra (till exempel Hilberts satslogiksystem) är snåriga att använda, men lämpar sig bättre vid till exempel induktionsbevis över härledningars längd.

Två önskvärda egenskaper hos härledningsssystem är sundhet och fullständighet.

Referenser

  • A. S. Troelstra, H. Schwichtenberg, Basic proof theory (2000), Cambridge University Press, ISBN 0-521-77911-1

Se även

Hämtad från "https://sv.rilpedia.org/wiki/H%C3%A4rledningssystem"
Personliga verktyg