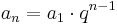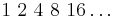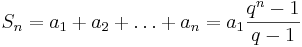Geometrisk följd
Från Rilpedia
En geometrisk följd är en talföljd där kvoten mellan ett element och det närmast föregående är konstant.
För att beräkna talet med ordningsnumret n används formeln
där q är kvoten.
Exempel på geometrisk talföljd
I detta exempel är kvoten q = 2 och det första talet a1 = 1.
Summan
Summan av de n första talen i en geometrisk talföljd 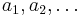 med kvoten
med kvoten 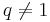 kan beräknas genom
kan beräknas genom
För en geometrisk serie gäller att den konvergerar om | q | < 1.