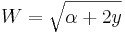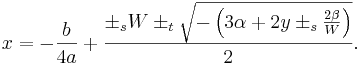Fjärdegradsekvation
Från Rilpedia

En fjärdegradsekvation är en ekvation som kan skrivas på formen
där a ≠ 0.
Fjärdegradsekvationen har alltid fyra lösningar (rötter) räknade med multiplicitet. Om koefficienterna a, b, c, d och e alla är reella tal kommer även antingen alla fyra lösningarna, två av lösningarna eller ingen av lösningarna vara reella tal.
Innehåll |
Bakgrund
Den allmänna fjärdegradsekvationen löstes först efter det att den generella lösningsskissen för tredjegradsekvationen tagits fram. Detta skedde på 1500-talet av Cardanos elev L. Ferrari, men publicerades av Cordano i Ars Magna år 1545. Själva principen i lösningsmallen för fjärdegradaren är att transformera den till en tredjegradsekvation för att sedan lösa den enligt den generella lösningsgången.
Lösningsskiss
Det enklaste sättet att lösa en fjärdegradsekvation är att hitta en rot (r) och sedan dividera ekvationen med x − r), för att på så sätt få en tredjegradsekvation som blir lättare att lösa.
Enklare fall
Begränsat fall
Om e (konstanttermen) = 0 så kommer även en av rötterna att vara x = 0, och övriga rötter kan då finnas genom att dividera polynomet med x och sedan lösa den tredjegradsekvation man då får.
Uppenbara rötter: 1, −1 och −k
Sätt vår fjärdegradsekvation som P(x). Då 1n = 1 så är P(1) = a + b + c + d + e. Därav följer att om a + b + c + d + e = 0 så är P(1) = 0 och därigenom är x = 1 en rot till P(x). På samma sätt gäller även att om a + c + e = b + d så är x = −1 en rot.
Om b är en multipel (k) av a, e är en multipel (k) av d och c = 0, så är även en x= −k en rot till ekvationen. Detta följer av att man skriver om ekvationen enligt följande:
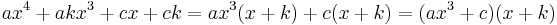 .
.
I samtliga tre exemplen så dividerar man polynomet med (x − 1), (x + 1) eller (x + k), vilket ger en tredjegradsekvation som sedan löses för att få fram övriga rötter.
Bikvadratisk ekvation
En fjärdegradsekvation där b och d är lika med 0 (alltså ax4 + cx2 + e = 0 löses enkelt genom ett variabelbyte (x2 = z), som ger oss en andragradsekvation az2 + cz + e = 0 som sedan löses på sedvanligt sätt. Observera att lösningen av az2 + cz + e = 0 ger oss 1 eller 2 rötter, som sedan vid insättning i x2 = z ger oss 2 eller 4 rötter.
Halvsymmetrisk ekvation
Om vår fjärdegradsekvation ser ut enligt följande, så har vi en halvsymmetrisk ekvation:
En halvsymmetrisk ekvation löses genom att första dela ekvationen med x 2 och sedan genomföra ett variabelbyte (z = x + m/x). Då får man åter igen en andragradsekvation som enkelt löses enligt gängse rutin.
Allmän lösning, enligt Ferraris modell
Ferrari fann en metod för att lösa fjärdegradsekvationer som klarar av att ta fram samtliga rötter, oavsett multiplicitet. Till att börja med så måste vi konvertera vår fjärdegradsekvation till en komprimerad fjärdegradsekvation.
Konvertering till en komprimerad fjärdegradsekvation
Börja med att dela båda leden i vår ekvation med a,
Första steget efter det blir att eliminera x3-termen. Detta görs genom ett variabelbyte (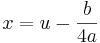 ). Då får man
). Då får man
Utvecklar man ekvationen så får man
Förenklar vi sedan uttrycket så får vi
Därefter byter vi namn på koefficienterna till u enligt följande:
Resultatet blir då
vilket är en komprimerad fjärdegradsekvation.
Om 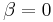 så har vi en Bikvadratisk ekvation, vilket enkelt löses enligt ovan.
så har vi en Bikvadratisk ekvation, vilket enkelt löses enligt ovan.
Om 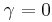 så är en av rötterna u = 0, vilket är ett begränsat fall, vilket också löses enkelt enligt ovan.
så är en av rötterna u = 0, vilket är ett begränsat fall, vilket också löses enkelt enligt ovan.
Ferrari's lösning
om både 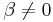 och
och 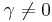 så kan vi lösa den komprimerade fjärdegradsekvationen enligt Lodovico Ferraris metod. När man väl har sin komprimerade fjärdegradsekvation så adderar man följande
så kan vi lösa den komprimerade fjärdegradsekvationen enligt Lodovico Ferraris metod. När man väl har sin komprimerade fjärdegradsekvation så adderar man följande
till ekvation (1), och får på så sätt
Målet med detta är att få en perfekt kvadrat i högerledet på ekvationen (u2 + α)2.
Nästa steg är att addera en variabel y i parentesen i vänstra ledet i ekvation (2), och en motsvarande 2y i koefficienten av u2-termen på högra sidan. För att lyckas med detta så använder vi oss av följande två samband i ekvation (2).
och
Adderar man dessa två samband så får man
som efter addition med ekvation (2) ger oss
vilket är ekvivalent med
Nu är nästa steg att välja ett värde på y så att det högra ledet av ekvationen (3) blir en perfekt kvadrat. Detta görs lättast genom att låta diskriminanten av den kvadratiska funktionen bli noll.
För att göra om det högra ledet av ekvationen (3) till en perfekt kvadrat, så måste följande ekvation lösas:
Multiplicera ihop parenteserna
Dividera båda sidorna med −4, och flytta −β2/4.
Vi har nu fått en tredjegradsekvation för y, i vilken vi delar båda leden med 2,
Genom ytterliggare ett variablebyte (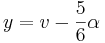 ) så blir ekvation (4)
) så blir ekvation (4)
Expandering och förenkling ger oss sedan följande ekvation:
Vi byter koefficienterna enligt följande:
Och får då följande tredjegradsekvation
Lösningarna på denna ekvation (5), (vilken som helst fungerar, så ta valfri komplex rot) räknas ut enligt följande:
där
och V räknas ut enligt definitionerna som − U3 − V3 = Q som − 3UV = P. Detta ger oss då att
Med y given av ekvation (6) så är det nu klart att det högra ledet av ekvation (3) är en perfekt kvadrat av formen
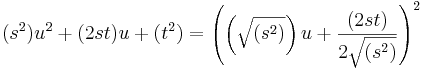
- (Detta är sant, oavsett vilket tecken man sätter framför rottecknen, så länga man sätter samma på bägge.)
Detta gör att vi kan skriva om den ekvation så här:
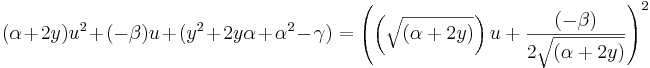 .
.
- Observera: Om β ≠ 0 så är α + 2y ≠ 0. Om β = 0 så skulle detta vara en bikvadratisk ekvation, vilket vi redan gått igenom.
Ekvation (3) kan därför skrivas så här:
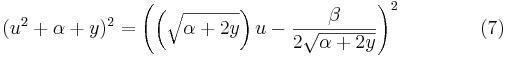 .
.
Förenkling, utveckling och samlande av termer ger oss sedan följande ekvation
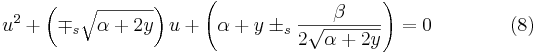 .
.
- Anmärkning: Index s i
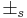 och
och 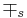 är där för att visa att de beror på varandra.
är där för att visa att de beror på varandra.
- Anmärkning: Index s i
Ekvation (8) är en andragradsekvation till u med följande lösning:
Förenklar vi denna lösning något så får vi slutligen följande:
Vilket ger oss lösningen på vår ursprungliga fjärdegradsekvation.
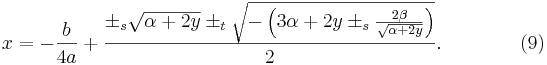
- Kom ihåg att de två
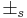 kommer från ekvation 8 och skall ha samma tecken, medan
kommer från ekvation 8 och skall ha samma tecken, medan 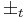 kan vara både plus och minus, oberoende av
kan vara både plus och minus, oberoende av 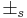 .
.
- Kom ihåg att de två
Sammanfattning av Ferrari's lösningsmetod
Om vi har en given ekvation:
så kan man få ut dess lösningar med hjälp av följande beräkningar:
Om 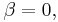 så får vi
så får vi
Om 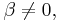 , så får vi istället:
, så får vi istället:
(Både plus och minus framför rottecknet fungerar.)
(Har tre komplexa rötter, vilken som av dessa fungerar)
-
- Båda ±s måste ha samma tecken medan ±t är oberende av de andra två. För samtliga lösningar, beräkna x med samtliga kombinationer av plus och minus för ±s och ±t.
Femtegradsekvationen?
Fjärdegradsekvationen är den ekvation av högst grad som är lösningsbar enligt en generell mall där endast de fyra räknesätten och rotutdragning används. Detta visade Paolo Ruffini, men då hans resonemang hade vissa brister har beviset tillskrivits Niels Henrik Abel, norsk matematiker. Abel bevisade snarare att femtegradsekvationen är omöjlig att lösa enbart genom algebraiska operationer.
Källor
- Weisstein, Eric W. "Quartic Equation." From MathWorld--A Wolfram Web Resource. mathworld.wolfram.com
- Thompson, Jan, Matematiklexikon (1991), Whalström och Widstrand, ISBN 91-46-16515-0


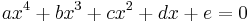
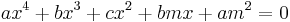
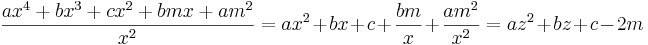
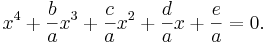
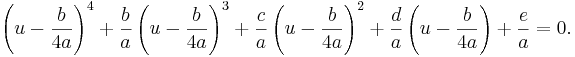
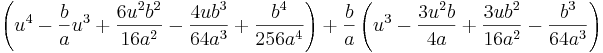
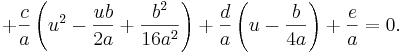
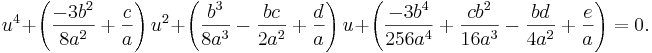
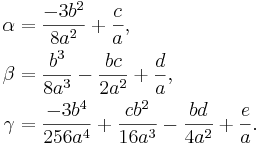
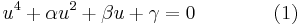
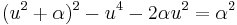
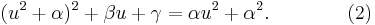
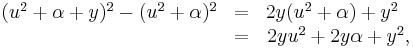
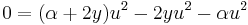
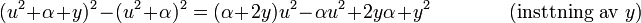
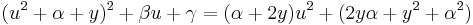
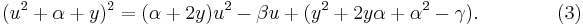
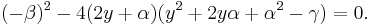
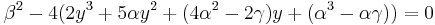
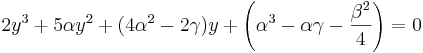
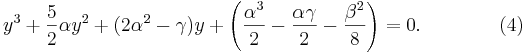
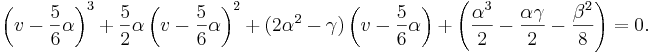
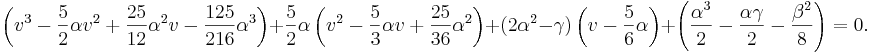
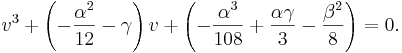
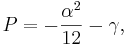
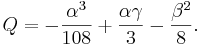
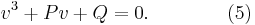
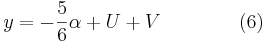
![U=\sqrt[3]{-{Q\over 2}\pm \sqrt{{Q^{2}\over 4}+{P^{3}\over 27}}}](/w/images/sv.rilpedia.org/math/b/6/f/b6f987f2ebbf25dc28f768e5138e1363.png)
![V=\begin{cases}
-\frac{P}{3U}&\text{ if }U\ne 0\\
-\sqrt[3]{Q}&\text{ if }U=0\ .
\end{cases}](/w/images/sv.rilpedia.org/math/4/e/9/4e9951c54023ef7d71b603a430795982.png)
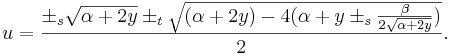
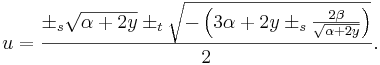
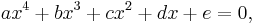
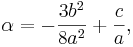
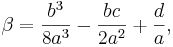
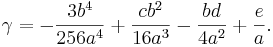
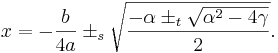
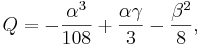
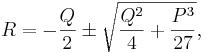
![U = \sqrt[3]{R},](/w/images/sv.rilpedia.org/math/e/3/3/e3322597c0d374ee70164f962ea53329.png)
![y = \begin{cases}
- {5 \over 6} \alpha + U - \frac{P}{3U} & \text{om }U\ne 0\\
-{5\over 6} \alpha - \sqrt[3]{Q} & \text{om }U=0
\end{cases}](/w/images/sv.rilpedia.org/math/c/a/8/ca8a3ace45b1a048fff76916572bb24a.png)