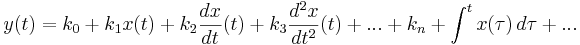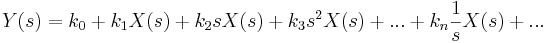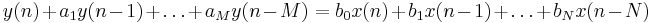Filter (signalbehandling)

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Filter är inom signalbehandingen ett byggblock som tar en signal som indata och ändrar dess spektrala egenskaper. Dessa används bland annat för att undertrycka brus och för att anpassa signaler till transmissionskanaler.

Innehåll

Filterkaraktäristik

Enkla filter kan delas in i fyra grupper, beroende på vilka frekvenser de stoppar och släpper igenom:

  • Lågpassfilter, som dämpar de höga frekvenserna,
  • Högpassfilter, som dämpar de låga frekvenserna,
  • Bandpassfilter, som dämpar både höga och låga frekvenser men inte området (bandet) däremellan, samt
  • Bandspärrfilter, som dämpar frekvenser inom ett område, men släpper igenom både högre och lägre frekvenser.

Ett filter kan också vara resonant, vilket i praktiken innebär att det framhäver frekvensområdena kring de bortfiltrerade frekvenserna.

Analoga filter

Med insignalen x(t) och utsignalen y(t) kan ett idealt filter ofta beskrivas med en linjär differentialekvation enligt:

y(t) = k_0 + k_1 x(t) + k_2 \frac{dx}{dt}(t) + k_3 \frac{d^2x}{dt^2}(t) + ... + k_n + \int^{t} x(\tau) \, d\tau + ...

Eftersom man är intresserad av frekvensinehållet gör man ofta en Laplacetransform och får sambandet:

Y(s) = k_0 + k_1 X(s) + k_2 s X(s) + k_3 s^2 X(s) + ... + k_n \frac{1}{s} X(s) + ...

Om man här sätter in s = jω där 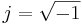j = \sqrt{-1} och ω är frekvensen uttryckt i radianer får man hur filtret reagerar på en sinusformad insignal med viss frekvens. En godtycklig insignal kan betrakats som en summa av sinussignaler med olika frekvens och amplitud, och utsignalen blir då motsvarande summa av utsignaler.

Ideala analoga filter är just ideala, de går inte att implementera i verkligheten. När analoga filter designas så måste en metods väljas beroende på vilken av filtrets egenskaper vi vill prioritera. Det finns tre huvudtyper:

Butterworthfilter är optimerat för att ge så lite rippel i passbandet som möjligt.

Tjebysjovfilter är konstruerat för att ge ett så smalt övergångsband som möjligt.

Besselfilter är designat för att ha en så optimalt linjär fasgång som möjligt.

Digitala filter

Digitala filter kan bland annat användas för att reducera brus i dataöverföringar eller för att utjämna frekvensfördelningen. De är även användbara inom områden som ljud- och musikteknik och grafikredigering.

Linjära filter

Ett linjärt, tidsdiskret och kausalt filter H kan skrivas som:

y(n) + a_1 y(n-1) + \ldots + a_M y(n-M) = b_0 x(n) + b_1 x(n-1) + \ldots + b_N x(n-N)

Efter z-transform:

A(z)Y(z) = B(z)X(z)
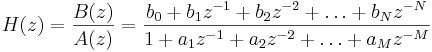
H(z) = \frac{B(z)}{A(z)} = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2} + \ldots + b_N z^{-N}} {1 + a_1 z^{-1} + a_2 z^{-2} + \ldots + a_M z^{-M}}

H är filtrets överföringsfunktion. Om A(z) = 1 och 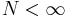N<\infty kallas H för ett FIR-filter. Om B(z) är konstant och nollskild så kallas H för autoregressivt.

Hämtad från "https://sv.rilpedia.org/wiki/Filter_(signalbehandling)"
Personliga verktyg