Eulers knäckningsfall
Från Rilpedia
Leonhard Euler var den förste som studerade knäckning, det vill säga balkteori för en stång som belastas med tryck i riktning ände mot ände. Han identifierade 4 olika knäckningsfall:
- Stångens ena ände fast inspänd, den andra fri. Knäckkraften blir i detta fall:
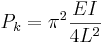
- Stångens båda ändar ledbart lagrade. Knäckkraften blir i detta fall: :
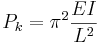
- Stångens ena ände fast inspänd, den andra ledbart lagrad. Knäckkraften blir i detta fall: :
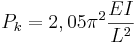
- Stångens båda ändar fast inspända. Knäckkraften blir i detta fall: :
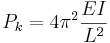
Man talar ibland om ett femte knäckningsfall som är ett specialfall av det fjärde, där stångens ena ände är fast inspänd i en vagn som tillåter en vinkelrät förskjutning mot stångens längdriktning. Den andra änden är fast inspänd. Knäckkraften blir i Eulers femte knäckningsfall:
I dessa formler är Pk Knäckkraften, E Elasticitetsmodulen för materialet, I balkens eller stångens böjtröghetsmoment och L balkens eller stångens längd.
Det visar sig att vad stången klarar av innan den knäcks blir väsentligen olika allt efter det sätt på vilket dess ändar är fastsatta.




