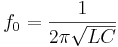Elektromagnetisk svängningskrets
Från Rilpedia
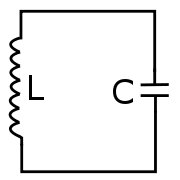
En elektromagnetisk svängningskrets eller resonanskrets är en elektrisk krets, där energi oscillerar mellan det elektriska fältet i en kapacitans C och det magnetiska fältet i en induktans L. En LC-krets är en idealiserad modell (av en RLC-krets), som förutsätter att det inte läcker ut energi till följd av resistans R.
I en sammankopplad sådan avstämd LC-krets kan en elektrisk ström svänga mellan komponenerna vid kretsens resonansfrekvens
Sådana LC -kretsar används flitigt antingen för att alstra signaler vid en viss bestämd frekvens, eller för att plocka ut en signal med särskild frekvens ur en mer komplex signal. De är nyckelkomponenter i många tillämpningar som oscillatorer, filter, frekvensblandare, tuner i receiver och antenner.
Innehåll |
Funktion
LC-kretsen kan lagra elektrisk energi, när den svänger vid sin resonansfrekvens. Kondensatorn lagrar energi i det elektriska fältet mellan sina plattor, i förhållande till spänningen över dem, medan spolen lagrar energi i dess magnetfält, beroende på den strömmen genom den. Om en uppladdad kapacitans ansluts över en induktans, så börjar laddning att flyta till induktansen, och den bygger upp ett magnetfält kring sig, vilket reducerar spänningen över kapacitansen. Till slut har all laddning i kapacitansen gått över. Strömmen fortsätter dock att flyta, eftersom spolar motsätter sig strömförändringar, varvid energi dras från det magnetiska fältet för att upprätthålla flödet. Det medför att strömmen börjar ladda kondensatorn med spänning av motsatt polaritet till dess ursprungliga laddning. När så magnetfältet är helt tömt, kommer strömmen att avstanna och laddningen är åter lagrad i kondensatorn (nu med motsatt polaritet) och cykeln kommer att sätta igång igen, med strömmen i omvänd riktning.
Se även
- Godhetstal
- Centerfrekvens
- Dipper (GDO, dipmätare)
- Heathkit