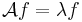Egenfunktion
Från Rilpedia
Inom matematiken, så är en egenfunktion till en linjär operator A definierad på något funktionsrum en funktion f (skild från nollfunktionen)
i funktionsrummet som av operatorn avbildas på en skalär multipel av sig själv. Mer precist, så gäller
för någon skalär, λ, det tillhörande egenvärdet.
Existensen av egenfunktioner är vanligen av stor hjälp för att förstå operatorn A.
Exempel
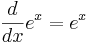 .
.
Alltså är 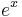 en egenfunktion till
en egenfunktion till 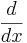 med egenvärdet λ = 1.
med egenvärdet λ = 1.
På samma sätt visar  att
att 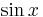 är en egenfunktion till
är en egenfunktion till 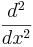 med egenvärdet λ = − 1.
med egenvärdet λ = − 1.