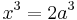Från Rilpedia

Deliska problemet, kubens fördubbling är en geometrisk uppgift, som mycket sysselsatte forntidens lärde och i vilken det gäller att beräkna kanten av den kub eller tärning, vars volym är dubbelt så stor som en given kubs (duplicatio cubi). Plutarchos berättar att, då en pest härjade Aten, oraklet på Delos gav de rådfrågande det svaret att man för att farsoten skulle upphöra, borde "fördubbla" Apollons kubformade altare. För att få veta sidlängden på det blivande altaret vände man sig till Platon, vilken, ur stånd att besvara frågan, förklarade att det guden mindre åsyftade var att hans altare skulle fördubblas, utan snarare att grekerna skulle vinnlägga sig om geometriens studium. Emellertid visar det sig att det inte med hjälp av konstruktionerna i euklidisk geometri går att fördubbla kuben. Detta kan visas genom att formulera problemet algebraiskt: Kalla den givna kubens kant a och den söktas x; de respektive kubernas volymer blir då a ³ och x ³, och följande likhet kan uppställas:

Man kan med hjälp av galoisteori visa att geometriska konstruktioner endast medger att sträckor vars längd beskrivs av ett tal som ligger i en kroppsutvidning av de rationella talen vars grad är en tvåpotens konstrueras, vilket innebär att sidan av ovanstående längs inte i allmänhet kan konstrueras.

Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 ^(Not).