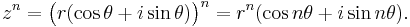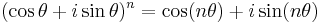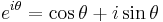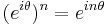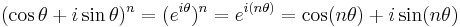de Moivres formel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

de Moivres formel, uppkallad efter Abraham de Moivre, är ett sätt att beräkna värdet av ett komplext tal upphöjt till ett heltal n, det vill säga 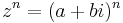z^n = (a + bi)^n \,. På polär form lyder formeln:

z^n = \bigl(r(\cos\theta+i\sin\theta)\bigr)^n = r^n(\cos n\theta + i\sin n\theta).

Uttryckt i naturligt språk betyder detta att man multiplicerar den polära formens vinkel med exponenten och upphöjer radien till exponenten för att få fram resultatet.

Bevis

Att bevisa de Moivres formel hänger på att visa

(\cos \theta + i \sin \theta)^n = \cos (n\theta) + i \sin (n\theta)\,

då resten av formeln följer av potenslagarna.

Med Eulers formel

Givet Eulers formel:

e^{i \theta} = \cos \theta + i \sin \theta \,

och följande exponentlag:

(e^{i\theta})^n = e^{in\theta}\,

följder det lätt att:

(\cos \theta + i \sin \theta)^n = (e^{i\theta})^n = e^{i(n\theta)} = \cos (n\theta) + i \sin (n\theta)\,
Hämtad från "https://sv.rilpedia.org/wiki/De_Moivres_formel"
Personliga verktyg