Cauchys medelvärdessats

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Cauchys medelvärdessats är en generalisering av Lagranges medelvärdessats.

Låt f och g vara två funktioner 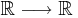$\mathbb{R} \longrightarrow \mathbb{R}$ med följande tre egenskaper.

Funktionerna f och g är kontinuerliga över ett slutet intervall $[a, \, b]$ .
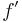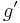Derivatorna $f^\prime$ och $g^\prime$ existerar över det öppna intervallet $(a, \, b)$ .
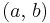Derivatan 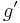$g^\prime$ är inte lika med noll på det öppna intervallet $(a, \, b)$ .

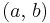Då innehåller det öppna intervallet 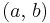$(a, \, b)$ minst ett tal, $c$ , för vilket följande ekvation är sann:

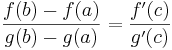$\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f^\prime(c)}{g^\prime(c)}$ .

Bevis

Cauchys medelvärdessats bevisas genom att tillämpa Rolles sats på följande linjärkombination av det två funktionerna f och g:

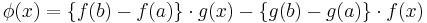$\phi(x) = \{f(b)-f(a)\} \cdot g(x) - \{g(b)-g(a)\} \cdot f(x)$ .

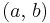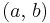De fakta att funktionerna f och g är kontinuerliga på det slutna intervallet $[a, \, b]$ och deriverbara på det öppna intervallet $(a, \, b)$ innebär att funktionen $φ$ är kontinuerlig på det slutna intervallet $[a, \, b]$ och deriverbar på det öppna intervallet $(a, \, b)$ ; dessutom antar funktionen samma värde i intervallets ändpunkter:

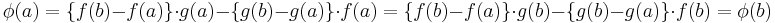$\phi(a) = \{f(b)-f(a)\} \cdot g(a) - \{g(b)-g(a)\} \cdot f(a) = \{f(b)-f(a)\} \cdot g(b) - \{g(b)-g(a)\} \cdot f(b) = \phi(b)$ .

Rolles sats säger då att det öppna intervallet 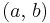$(a, \, b)$ innehåller ett tal, c, för vilket derivatan 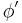$\phi^\prime$ antar värdet noll:

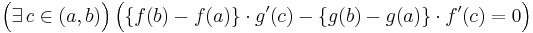$\Big( \exists \, c \in (a,b) \Big) \, \Big(\{f(b)-f(a)\} \cdot g^\prime(c) - \{g(b)-g(a)\} \cdot f^\prime(c) = 0 \Big)$ .

Vi gör nu följande två observationer rörande funktionen g.

Vi vet att derivatan 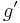$g^\prime$ inte är noll på det öppna intervallet 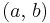$(a, \, b)$ vilket innebär att talet 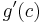$g^\prime(c)$ inte är lika med noll.
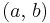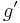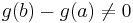Om funktionen g antar samma värde i intervallets ändpunkter så kan vi tillämpa Rolles sats på den, och hävda att intervallet $(a, \, b)$ innehåller ett tal där derivatan $g^\prime$ är lika med noll; men detta strider mot vad vi vet om funktionen g. Därför antar den inte samma värde i intervallets ändpunkter, varför differensen $g(b)-g(a) \neq 0$ .

Dessa observationer låter oss dividera ekvationen 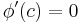$\phi^\prime(c) = 0$ med talet 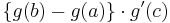$\{g(b)-g(a)\} \cdot g^\prime(c)$ – som vi nu vet inte är lika med noll – för att få följande resultat:

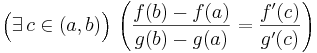$\Big( \exists \, c \in (a,b) \Big) \, \left( \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f^\prime(c)}{g^\prime(c)} \right)$ .

Detta avslutar beviset av Cauchys medelvärdessats.

Cauchys medelvärdessats

Från Rilpedia

Bevis

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda