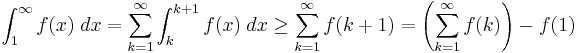Cauchys integralkriterium
Från Rilpedia
Cauchys integralkriterium används inom matematiken till att avgöra om en talserie är konvergent eller inte genom att jämföra med motsvarande integral.
Om 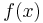 är positiv och avtagande på intervallet
är positiv och avtagande på intervallet 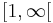 gäller att
gäller att
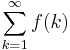 är konvergent om och endast om
är konvergent om och endast om 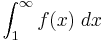 är det
är det
Bevis
Eftersom f(x) är avtagande gäller 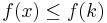 om
om 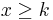 . Alltså gäller
. Alltså gäller
Dvs om serien är konvergent är integralen konvergent
På samma sätt gäller
Dvs om integralen är konvergent är serien konvergent
Alltså är serien konvergent om och endast om integralen är konvergent
Exempel
Den harmoniska serien
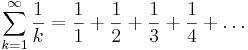 är konvergent om och endast om
är konvergent om och endast om 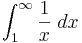 är det. Detta är dock inte fallet, eftersom
är det. Detta är dock inte fallet, eftersom![\int_{1}^{\infty} \frac{1}{x} \;dx = \left[\ln x\right]_1^{\infty} = \infty\](/w/images/sv.rilpedia.org/math/f/9/8/f987783c22dec6a76d2b3d141bb7ca43.png)




![\int_{k}^{k+1} f(x) \;dx \leq \int_{k}^{k+1} f(k) \;dx = \left[f(k) \cdot x\right]_{k}^{k+1} = f(k).](/w/images/sv.rilpedia.org/math/a/2/1/a21ad1f4c0ee3ab119874531b3e69141.png)
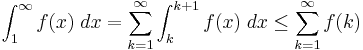
![\int_{k}^{k+1} f(x) \;dx \geq \int_{k}^{k+1} f(k+1) \;dx = \left[f(k+1) \cdot x\right]_{k}^{k+1} = f(k+1).](/w/images/sv.rilpedia.org/math/3/6/f/36fb5964f77c9a4f2d88daeb64980a01.png)