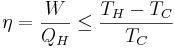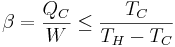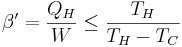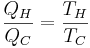Från Rilpedia

En värmemaskin är en anordning som utnyttjar en skillnad i temperatur för att utföra ett arbete.

Om man har två värmereservoarer vid temperaturerna T_H och T_C (Hot och Cold med T_H>T_C) där man vill utnyttja temperaturskillnaden för att utföra ett arbete W, så är det inte möjligt att omvandla all värme till arbete. Det bryter mot termodynamikens andra lag.

Däremot kan man bygga en maskin som tar ut en mängd värme Q_H ur den varma reservoaren, omvandlar en del till arbete W och överför resterande del Q_C till den kalla reservoaren. Maskinens verkningsgrad anger hur stor andel av den uttagna värmeenergin Q_H som blir arbete. Denna verkningsgrad kan tecknas som

Värmepumpar och kylmaskiner

Samma process som driver värmemaskinen kan även köras baklänges för att skapa en värmepump eller en kylmaskin. Det kan illustreras av figuren för värmemaskinen om man byter riktning på alla pilarna. Vi tillför alltså arbete för att värma kroppen märkt T_H samtidigt kroppen märkt T_C kyls. Ett kylskåp avger värme till rummet utanför samtidigt som det kyler maten. Värmepump och kylmaskin är egentligen samma sak, skillnaden är bara om det är den kylande eller värmande aspekten som vi är mest intresserade av.

En kylmaskin har en köldfaktor som anger hur mycket värmeenergi vi kan föra bort i relation till det arbete vi tillför. Den kan tecknas

Värmepumpen har på motsvarande sätt en värmefaktor som anger hur mycket värmeenergi vi kan få fram i relation till det arbete vi tillför. Den kan tecknas

Carnotprocesser

En carnotprocess är en tänkt, ideal process där likhet gäller i alla olikheter i formlerna för verkningsgrad. Den består av fyra processteg, oberoende av hur mekanismen ser ut i detalj. Här nedan ges processen i en värmemaskin, för värmepumpar och kylmaskiner kastas ordningen om:

1. En isoterm process vid temperaturen T_H, där systemets entropi ökar från S_H till S_C.
2. En reversibel, adiabatisk process där temperaturen sänks från T_H till T_C.
3. En isoterm process där entropin återigen sänks till S_H.
4. En reversibel, adiabatisk process där temperaturen återigen höjs till T_H, vilket för systemet tillbaka till ursprungsläget.

Detta ger Q_H=T_H(S_H-S_C) och Q_C=T_C(S_H-S_C) och därmed även

För värmepumpar och kylmaskiner medför detta att

Detta innebär att samma maskin är effektivare som värmepump än som kylmaskin, eftersom själva arbetet som stoppas in i den omvandlas till värme och därmed bidrar till effektiviteten.

Källor

• Mandl, F: Statistical Physics, Jown Wiley & Sons, Ltd, Chichester, England 1999. ISBN 0-471-91533-5.