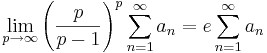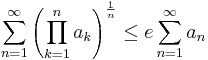Carlemans olikhet
Från Rilpedia
Carlemans olikhet är en matematisk olikhet namngiven efter Torsten Carleman, som var den förste att publicera olikheten 1923[1].
Låt a1,a2,... vara en följd av icke-negativa reella tal då det gäller att
Konstanten e i olikheten är den bästa möjliga; för mindre konstanter gäller inte olikheten. Om a1,a2... är positiva istället för icke-negativa är olikheten strikt.
Bevis
Utgå från Hardys olikhet:
ta den inre summan i vänsterledet, ersätt ak med 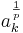 och skriv om på följande sätt:
och skriv om på följande sätt:
Låt 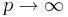 och skriv om exponenten som en derivata av den nya variabeln x, som här är noll:
och skriv om exponenten som en derivata av den nya variabeln x, som här är noll:
Applicera nu x = 0 då man får:
Betrakta nu högerledet i Hardys olikhet och utför samma steg, ersätt 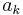 med
med 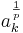 och låt p gå mot oändligheten
och låt p gå mot oändligheten
detta ger oss den icke-strikta varianten av Carlemans olikhet:
Fotnoter
- ↑ T. Carleman, Sur les fonctions quasi-analytiques, Conférences faites au cinquième congres des mathématiciens Scandinaves, Helsinki (1923), 181-196.
Referenser
- Maria Johansson, Lars-Erik Persson, Anna Wedestig, Carleman's inequality - history, proofs and som new generalizations (2003) Journal of Inequalities in Pure and Applied Mathematics. 4. (3). På internet 2009-02-10.




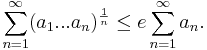

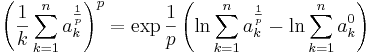
![\lim_{p \to \infty} \exp \frac{1}{p} \left(\ln \sum_{k = 1}^n a_k^\frac{1}{p} - \ln \sum_{k=1}^n a_k^0\right) =
\exp \left( \left[ \frac{d}{dx} ( \ln \sum_{k=1}^n a_k^x ) \right]_{x=0} \right)=
\exp \left( \left[ \frac{\sum_{k=1}^n a_k^x \ln a_k}{\sum_{k=1}^n a_k^x} \right]_{x=0} \right)](/w/images/sv.rilpedia.org/math/f/1/d/f1d6a1fb709db27d0ffdf5897b2f5c1c.png)
![\exp \left( \left[ \frac{\sum_{k=1}^n a_k^x \ln a_k}{\sum_{k=1}^n a_k^x} \right]_{x=0} \right)=
\exp\left(\frac{1}{n} \sum_{k=1}^n \ln a_k \right) = \left( \prod_{k=1}^n a_k \right)^\frac{1}{n}.](/w/images/sv.rilpedia.org/math/c/f/f/cffd3c038e4f2bff88092c1ac2d1fbb9.png)