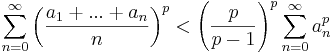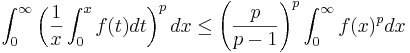Hardys olikhet

Från Rilpedia

Texten från svenska Wikipedia

Hardys olikhet är en matematisk olikhet uppkallad efter G.H. Hardy som säger att om $a 1, a 2, a 3,...$ är en talföljd av icke-negativa tal med något element skilt från noll så gäller det att:

$\sum_{n=0}^\infty \left( \frac{a_1 + ... + a_n}{n} \right)^p < \left( \frac{p}{p-1} \right)^p \sum_{n=0}^\infty a_n^p$

för varje positivt reellt tal $p > 1$ .

En integralversion av Hardys olikhet säger att om f är en integrerbar funktion med icke-negativa värden så gäller:

$\int_0^\infty \left( \frac{1}{x} \int_0^x f(t) dt \right)^p dx \leq \left( \frac{p}{p-1} \right)^p \int_0^\infty f(x)^p dx$

med likhet om och endast om $f (x) = 0$ nästan överallt.

Hardys olikhet

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk